Bond Riding the Yield Curve Strategy

I. What is the Riding Strategy?

The riding strategy is an active investment approach that capitalizes on the positive slope of the yield curve by holding medium- to long-term bonds until their remaining maturity shortens, thereby realizing capital gains. Its core logic is:

• Long-term bond yields are typically higher than short-term bond yields (upward-sloping yield curve).
• As time passes, the bond's remaining maturity decreases, and its yield slides down the curve, naturally driving up its price.
• Investors "ride" the yield curve to earn interest income + capital gains during the holding period.

Riding the Yield Curve

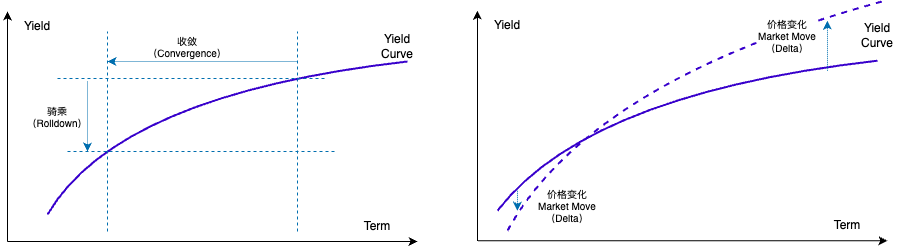
II. Breakdown of Riding Strategy Returns

According to standard market terminology, the total return of the riding strategy can be decomposed into the following five components:

1. Coupon Income

• Definition: The sum of periodic coupon payments received during the holding period.
• Quantification:

  $$\text{Coupon} = \sum_{i:\,t_i\in(t_0,t_1]} C_i$$

  where (C_i) is the (i)-th coupon payment, and ((t_0,t_1]) is the holding period.

2. Convergence Return

• Definition: Assuming the bond's yield-to-maturity (YTM) remains unchanged, the price convergence toward par (or a benchmark price) due solely to the reduction in remaining maturity from (T) to (T-\Delta t).
• Quantification:

  $$\Delta P_{\rm cvg} = P\bigl(Y_0,\;T-\Delta t\bigr)\;-\;P\bigl(Y_0,\;T\bigr)$$

  Both terms are priced at the same YTM (Y_0) but for different remaining maturities.

3. Rolldown Return

• Definition: Under the assumption that the shape and level of the yield curve remain unchanged, the bond's remaining maturity "rolls down" the curve—i.e., as (T)→(T-\Delta t), the corresponding YTM shifts from (Y_0) → (Y_{T-\Delta t}), leading to additional price appreciation.
• Quantification (slope effect only):

  $$\Delta P_{\rm rd} = P\bigl(Y_{T-\Delta t},\;T-\Delta t\bigr) \;-\; P\bigl(Y_0,\;T-\Delta t\bigr)$$

• Interpretation: Rolldown = Convergence + this slope effect.
• Example: Buying a 5-year bond (YTM=4%), after 1 year, the remaining maturity is 4 years. If the 4-year yield drops to 3.5%, the price difference (97.16 - 95.62 = 1.54) is the rolldown return.

4. Reinvestment Return

• Definition: The additional income earned by reinvesting coupon payments received during the holding period at prevailing market rates until the end of the holding period.
• Quantification: If the (i)-th coupon received at (t_i) is reinvested at rate (r_{\rm reinv}(t_i)) until (t_1),

  $$\text{Reinv} = \sum_{i:\,t_i\in(t_0,t_1]} C_i \times \bigl(1 + r_{\rm reinv}(t_i)\bigr)^{\,t_1 - t_i} \;-\; C_i$$

5. Market Move Impact

• Definition: The price difference caused by actual changes in the yield curve (parallel shifts, steepening/flattening, etc.) from (\mathcal Y_0) to (\mathcal Y_1) by the end of the holding period.
• Quantification:

  $$\Delta P_{\rm mkt} = P\bigl(Y_1,\;T-\Delta t\bigr) \;-\; P\bigl(Y_{T-\Delta t},\;T-\Delta t\bigr)$$

• Risk Attribute: Uncontrollable market risk that may offset or amplify rolldown returns.

6.Total Return Formula:

$$\underbrace{\sum C_i}_{\text{Coupon}} +\underbrace{\Delta P_{\rm cvg}}_{\text{Convergence}} +\underbrace{\Delta P_{\rm rd}}_{\text{Rolldown}} +\underbrace{\text{Reinv}}_{\text{Reinvestment}} +\underbrace{\Delta P_{\rm mkt}}_{\text{Market Move}}$$

III. Carry and Roll-down

In practice, Carry and Roll-down are the two most common ways to split a bond’s holding-period return:

1. Carry (Holding Return)

   • Definition: The net coupon income earned over the holding period, after deducting funding (repo) costs. Any reinvestment return on received coupons is also included here.
   • Components:
     • Coupon income
     • Reinvestment return
     • (If applicable) Minus funding cost

2. Roll-down (Riding Return)

   • Definition: Assuming the yield curve stays unchanged, the price change caused solely by the bond’s remaining maturity shortening from (T) to (T-\Delta t). This comprises two effects:
     • Pull-to-Par: At a fixed YTM, as a bond approaches maturity its price converges toward par.
     • Rolldown Return: On the same curve, different remaining maturities imply different YTMs; the price difference due to maturity shortening.

3. Carry + Roll-down = Total Capital Gain
   Ignoring market shifts, the expected one-year return on a two-year bond roughly equals the one-year forward rate one year out:

   $$f_1 \approx \frac{(1+S_2)^2}{(1+S_1)} - 1 \approx \underbrace{S_2 - \text{Funding}}_{\text{Carry}} + \underbrace{(S_2 - S_1)}_{\text{Roll-down}}$$

Key points:

• Defining Carry as “coupon + reinvestment – funding” and Roll-down as “pull-to-par + slope roll” helps you accurately measure holding-period returns in different market environments.
• With an inverted curve, long-end carry is often negative, and roll-down may be limited because short-end yields exceed long-end yields.

. Detailed Calculation of Rolldown Return

Core Assumption

• The shape and level of the yield curve remain unchanged (only the bond's maturity shortens, and YTM slides down the curve).

Calculation Steps

1. Initial Price (Purchase Time)
   Calculate the full price (including accrued interest) based on the bond's remaining maturity and the current yield curve.
   Formula:

   $$P_0 = \sum \frac{C}{(1+YTM)^t} + \frac{Face\ Value}{(1+YTM)^T}$$

   This can be understood as calculating the full price using the yield, if the yield is known.

2. Future Price (After Holding)
   Recalculate the full price using the new YTM corresponding to the shortened remaining maturity.
   Example:

   • Initial: 5-year bond, YTM=4%, price=95.62.
   • After 1 year: Remaining maturity=4 years, YTM slides to 3.5%, price=97.16.
   • Rolldown Return = 97.16 - 95.62 = 1.54.

Key Influencing Factors

• Slope of the Yield Curve: The steeper the curve, the higher the rolldown return.
• Bond Convexity: Bonds with higher convexity are more sensitive to yield declines.