Construction of the FX Options Volatility Surface

Visit the Mathema Option Pricing System for FX options and structured product pricing and valuation!

Introduction

In the FX options market, implied volatility is a key parameter for pricing and risk management. Since the implied volatility of options typically exhibits a non-flat curve that varies with strike prices and maturities, traders and risk managers need to construct a "volatility surface" to visually represent the distribution of implied volatilities. This supports option pricing, hedging, and risk management.

The construction of the volatility surface relies on several core concepts, among which Delta and ATM Types are fundamental metrics. These are used to measure the sensitivity of option prices to changes in the underlying price and to determine the center point of the volatility surface, respectively. This article will detail these core concepts and explain their roles in constructing the volatility surface.

1. Sources of FX Volatility

1.1 Market Volatility Quotation Format

In the FX options market, volatility is typically quoted in Delta/Vol rather than Strike/Vol. This is because the FX market focuses more on Delta (measuring the sensitivity of option prices to changes in the underlying asset price) than on strike prices. This quotation format provides a more intuitive reflection of the market's demand for volatility across different risk exposures.

The market volatility quotation format is usually Tenor/DeltaString/Vol, which includes the following elements:

Tenor (Maturity):
Represents the option's time to maturity, e.g., 1 week (1W), 1 month (1M), 1 year (1Y), etc.
DeltaString (Delta Type):
Volatility quotes for different Delta types, e.g., 10RR (10 Delta Risk Reversal), 25RR (25 Delta Risk Reversal), ATM (At-The-Money), etc.
Vol (Volatility):
Implied volatility data corresponding to the Delta type.

1.2 Key Parameters in Volatility Quotations

Market volatility quotations typically include the following parameters:

ATM (At-The-Money):
The implied volatility of at-the-money options, serving as the benchmark for the volatility surface.
ATM volatility is the baseline value for constructing the volatility surface, representing the market's expectation of implied volatility for at-the-money options. Market conventions define ATM volatility as ATM-Spot, ATM-Forward, or ATM-Delta-Neutral.
RR (Risk Reversal):
The difference between the implied volatilities of call and put options at the same Delta, used to measure the market's demand for directional risk. Common RRs include 10RR and 25RR.
Risk Reversal is a measure of the relative demand for call and put options, defined as the difference between the implied volatilities of call and put options at the same Delta:

RR = \sigma_{call} - \sigma_{put}

Common RR quotations in the market include:

25RR: The volatility difference between 25 Delta call and put options.
10RR: The volatility difference between 10 Delta call and put options.

The sign of RR reflects market preferences:

Positive RR: The market favors hedging against upside risks (higher demand for call options).
Negative RR: The market favors hedging against downside risks (higher demand for put options).
BF (Butterfly):
The weighted difference between the implied volatilities of off-Delta options and ATM volatility, used to measure the steepness of the volatility smile. Common BFs include 10BF and 25BF.
Butterfly measures the market's demand for the shape of the volatility smile, defined as the weighted difference between the implied volatilities of off-Delta options and ATM volatility:

BF = \frac{\sigma_{call} + \sigma_{put}}{2} - \sigma_{ATM}

Common BF quotations in the market include:

25BF: The shape of the volatility smile at 25 Delta.
10BF: The shape of the volatility smile at 10 Delta.

The value of BF reflects the steepness of the volatility surface:

Positive BF: A steeper volatility smile, with higher implied volatilities for out-of-the-money options.
Negative BF: A flatter volatility smile.

1.3 Practical Volatility Quotation Format

In summary, the FX options market typically quotes volatility in the following format:

ATM volatility
25RR, 10RR
25BF, 10BF

This format provides the core parameters for constructing the volatility surface. RR and BF describe the asymmetry and steepness of the volatility smile, while ATM volatility provides the benchmark point for the surface.

Below is an example of actual volatility quotations, showing volatility data for different tenors and Delta strings: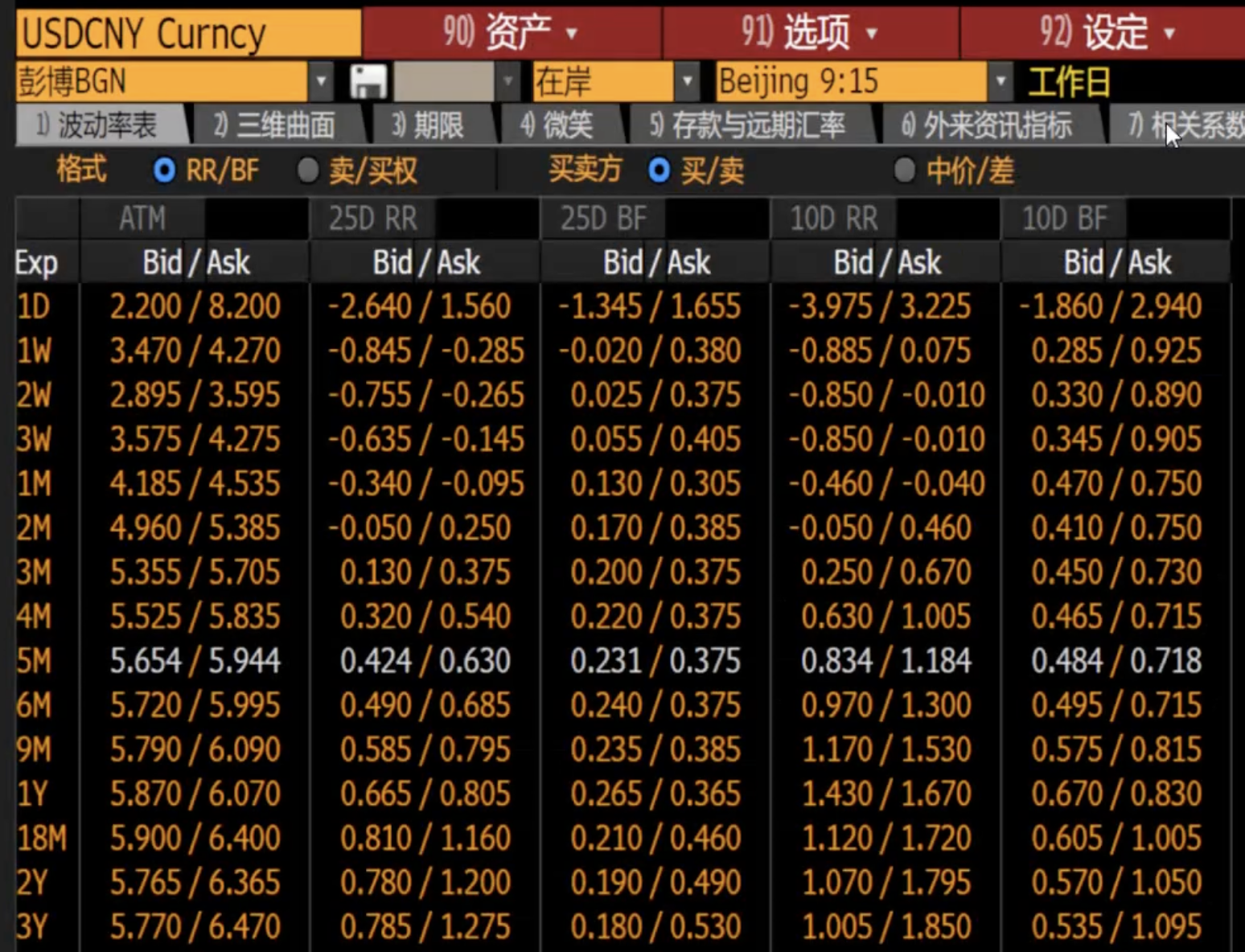

1.4 Significance of Volatility Quotations

The above volatility quotation table has the following significance:

ATM Volatility:
Provides the benchmark point for constructing the volatility surface, reflecting the market's expectation of neutral risk.
RR and BF:
Describe the asymmetry and steepness of the volatility smile, reflecting the market's preference for upside or downside risks.
Term Structure:
Volatility data across different maturities reflects the market's expectations for short-term and long-term volatility. Short-term volatility is often driven by events, while long-term volatility reflects the market's long-term volatility expectations.

Using these quotations, traders can construct a complete volatility surface, supporting option pricing and risk management.

2. Premium Types (Premium Adjusted)

Generally, the premium is in the term currency. For cases where the premium is quoted in the base currency, special adjustments are required when converting between Delta, strike, and volatility.

3. Types of Delta (Delta Types)

3.1 Importance of Delta

Delta is a key metric for measuring the sensitivity of option prices to changes in the underlying asset price. It is not only a core parameter in option pricing but also used for hedging and risk management. In the FX options market, the definition of Delta differs from that in the equity market, primarily because the value of FX options can be denominated in two currencies (domestic and foreign). Below are the three common types of Delta in the FX market.

3.2 Spot Delta ( $\Delta_S$ )

Spot Delta is the first derivative of the option price with respect to the spot price $S_t$ , representing the amount of the underlying asset needed to hedge the option position in the spot market.

Formula:

Delta_S = \phi e^{-r_f \cdot \tau} N(\phi d_+)

where:

$\phi = +1$ for call options, $\phi = -1$ for put options.
$r_f$ : Foreign risk-free rate.
$\tau$ : Time to maturity.
$d_+ = \frac{\ln\left(\frac{f(t, T)}{K}\right) + \frac{1}{2} \sigma^2 \tau}{\sigma \sqrt{\tau}}$

3.3 Forward Delta ( $\Delta_f$ )

Forward Delta is the first derivative of the option price with respect to the forward price $f(t, T)$ , representing the amount of the forward contract needed to hedge the option position in the forward market.

Formula:

Delta_f = \phi N(\phi d_+)

The difference from Spot Delta is that Forward Delta does not include the discount factor $e^{-r_f \cdot \tau}$ .

3.4 Premium-Adjusted Delta ( $\Delta_{pa}$ )

Premium-Adjusted Delta accounts for the impact of the option price on the hedging position, adjusting Spot Delta or Forward Delta.

Formula:

Spot Premium-Adjusted Delta:
$Delta_{S, pa} = \Delta_S - \frac{v}{S_t}$
where $v$ is the option price (in domestic currency).
Forward Premium-Adjusted Delta:
$Delta_{f, pa} = \phi \frac{K}{f} N(\phi d_-)$
where:
$d_- = \frac{\ln\left(\frac{f}{K}\right) - \frac{1}{2} \sigma^2 \tau}{\sigma \sqrt{\tau}}$

4. ATM Types

At-The-Money (ATM) defines the center point of the implied volatility surface and is a crucial benchmark for constructing the volatility surface. The FX market has multiple ATM definitions, catering to different trading needs and market environments.

4.1 ATM-Spot

Definition:

Strike price equals the spot price:

K_{ATM} = S_t

4.2 ATM-Forward

Definition:

Strike price equals the forward price:

K_{ATM} = f(t, T)

where:

f(t, T) = S_t \cdot e^{(r_d - r_f) \cdot \tau}

4.3 ATM-Value-Neutral

Definition:

Ensures that the prices of call and put options are equal:

v(S_t, K_{ATM}, \sigma, +1) = v(S_t, K_{ATM}, \sigma, -1)

4.4 ATM-Delta-Neutral

Definition:

Ensures that the absolute values of the call and put Deltas are equal:

Delta_{call} + \Delta_{put} = 0

4.5 Detailed Formula Table for ATM Types

The table below shows the formulas for Spot Delta, Forward Delta, Spot Premium-Adjusted Delta, and Forward Premium-Adjusted Delta under different ATM types:

Delta Type	ATM Δ-Neutral Strike	ATM Fwd Strike	ATM Δ-Neutral Delta	ATM Fwd Delta
Spot Delta	$f \cdot e^{\frac{1}{2}\sigma^2 \tau}$	$f$	$\frac{1}{2} \phi e^{-r_f \tau}$	$\phi e^{-r_f \tau} N(\phi \frac{1}{2} \sigma \sqrt{\tau})$
Forward Delta	$f \cdot e^{\frac{1}{2}\sigma^2 \tau}$	$f$	$\frac{1}{2} \phi$	$\phi N(\phi \frac{1}{2} \sigma \sqrt{\tau})$
Spot Delta p.a.	$f \cdot e^{-\frac{1}{2}\sigma^2 \tau}$	$f$	$\frac{1}{2} \phi e^{-r_f \tau} e^{-\frac{1}{2} \sigma^2 \tau}$	$\phi e^{-r_f \tau} N(-\phi \frac{1}{2} \sigma \sqrt{\tau})$
Forward Delta p.a.	$f \cdot e^{-\frac{1}{2}\sigma^2 \tau}$	$f$	$\frac{1}{2} \phi e^{-\frac{1}{2} \sigma^2 \tau}$	$\phi N(-\phi \frac{1}{2} \sigma \sqrt{\tau})$

5. Construction of the Volatility Surface

5.1 Delta-Based Volatility Surface

In the FX options market, implied volatility is typically quoted based on Delta rather than strike prices. The volatility surface uses Delta as the x-axis and time to maturity as the y-axis to construct a three-dimensional volatility distribution. By using the Delta types and ATM definitions discussed in this article, the volatility surface can be aligned with market realities.

5.2 Key Steps

Select Delta Type:
Choose Spot Delta, Forward Delta, or Premium-Adjusted Delta based on trading needs. Forward Delta is the most commonly used type.
Select ATM Definition:
Determine the center point of the volatility surface, e.g., using ATM-Forward or ATM-Delta-Neutral.
Convert Delta to Strike Price:
For a given Delta and implied volatility, calculate the corresponding strike price using the formula.
- For non-premium-adjusted (premium adjusted = false) Forward Delta:
  $K = f \cdot \exp\left(-\phi \cdot \sigma \cdot \sqrt{\tau} \cdot N^{-1}(\phi \Delta_f) + \frac{1}{2} \sigma^2 \tau \right)$
- For Spot Delta:
  $K = f \cdot \exp\left(-\phi \cdot \sigma \cdot \sqrt{\tau} \cdot N^{-1}\left(\frac{\phi \Delta_S}{e^{-r_f \cdot \tau}}\right) + \frac{1}{2} \sigma^2 \tau \right)$
Interpolation and Smoothing:
Use interpolation methods to smooth the volatility surface, ensuring continuity and smoothness in three-dimensional space.
Reference: FX Volatility Surface Interpolation Methods

6. Term Direction - "Linear Variance Interpolation (or Linear Interpolation of Variance × Term)"

Variance Accumulates Linearly Over Time
A common assumption in financial theory is that variance accumulates linearly over time. That is, if we let $\sigma$ denote the annualized volatility and $T$ denote the annualized term, the variance used in option pricing is typically expressed as $\sigma^2 \times T$ .
- Therefore, performing linear interpolation solely on the volatility itself may lead to distortions as the term extends.
- A more reasonable approach is to perform linear interpolation on $\sigma^2 \times T$ along the term axis, ensuring that the cumulative increase in variance aligns more closely with theoretical assumptions as the term lengthens.
Operational Steps
- First, calculate the annualized volatility $\sigma$ for each key term point.
- Then, convert it into variance ( $\sigma^2 \times T$ ).
- Perform linear interpolation on these variance points across the term span. For any given term $T^*$ , the interpolated variance $\sigma^2_{\text{interp}} \times T^*$ can be obtained.
- Finally, convert the interpolated variance back to annualized volatility using $\sigma_{\text{interp}} = \sqrt{\frac{\sigma_{\text{interp}}^2 \times T^*}{T^*}}$ .
Performing linear interpolation on variance (or $\sigma^2 \times T$ ) is the most typical and commonly used method for constructing the foreign exchange volatility surface in the term direction.