Foreign Exchange Options Greeks (Greek Letters) Complete Guide
Foreign Exchange Options Greeks (Greek Letters) Complete Guide
Visit the Mathema Option Pricing System, supporting FX options and structured product pricing and valuation!
Basic Concepts
'Greek letters' represent quantities that measure the sensitivity of an option's premium. They are used to predict the risk of an option contract.
- Delta - The change in the option premium relative to the change in the underlying currency pair price
- Gamma - Measures the rate of change of Delta (Δ) when the underlying currency pair price changes
- Vega - Measures how the option premium of the underlying currency pair is affected by changes in volatility (σ)
- Theta - Measures the sensitivity of the option premium to the passage of time (τ), or "time decay"
- Rho - Measures the sensitivity of the option premium to changes in interest rates (r)
Detailed Explanation of Core Greeks
Delta
Delta is the change in the option premium relative to the change in the underlying asset price.
How much the option value changes when the exchange rate moves by 1 unit.
Example: 50 Call Option, 90 days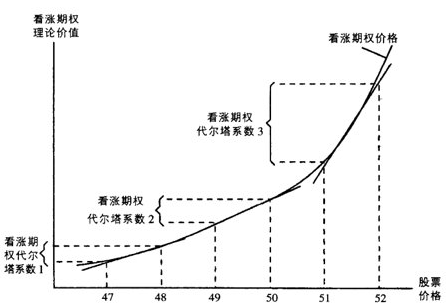
From the perspective of exercise probability, Delta indicates the likelihood of a vanilla option being exercised at expiration (reflecting the probability of the option expiring in-the-money).
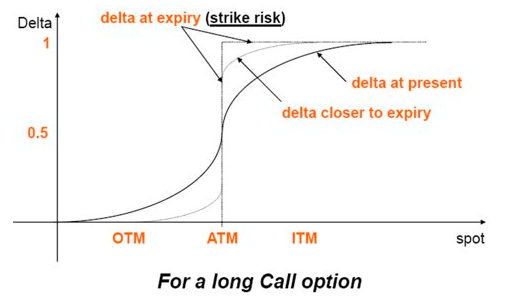
Taking a long call option as an example, as expiration approaches, the Delta of an ITM option will approach 1, and the Delta of an OTM option will approach 0.
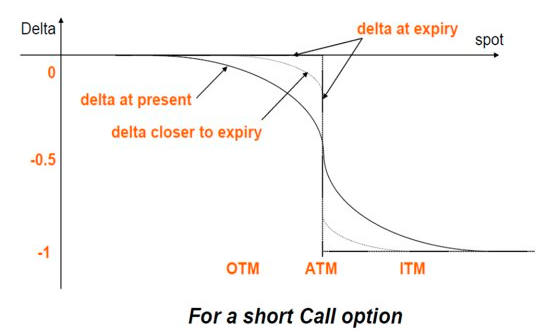
Taking a short call option as an example, as expiration approaches, the Delta of an ITM option will approach -1, and the Delta of an OTM option will approach 0.
Gamma Coefficient – The Rate of Change of Delta
Gamma :
Measures the rate of change of Delta (Δ) when the underlying currency pair price changes. The question here is: After a change in the spot price, how much will the Delta change?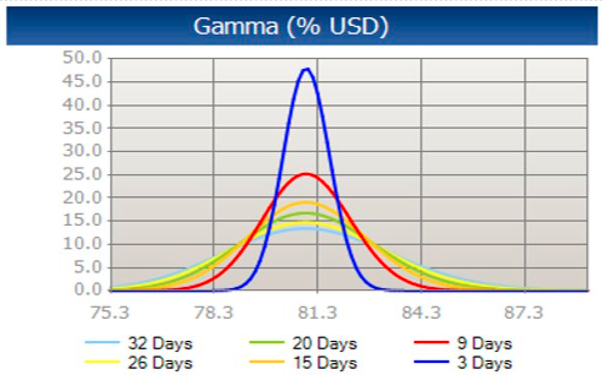
Gamma values can be positive or negative. A positive Gamma means the option's Delta will increase as the underlying asset price rises and decrease as the underlying asset price falls; a negative Gamma means the Delta will decrease as the underlying asset price rises and increase as the underlying asset price falls.
Generally, all long options have positive Gamma values, and all short options have negative Gamma values.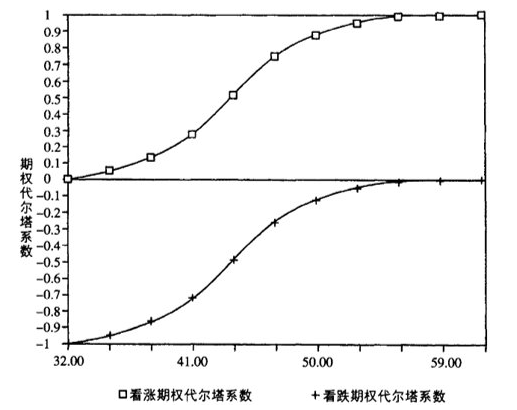
Theta Coefficient – Time Decay
Theta :
Measures the sensitivity of the option premium to the passage of time (τ), or "time decay." As the option contract approaches its expiration date, time decay accelerates.
- Theta is negative for long call and long put options, and positive for short call and short put options.
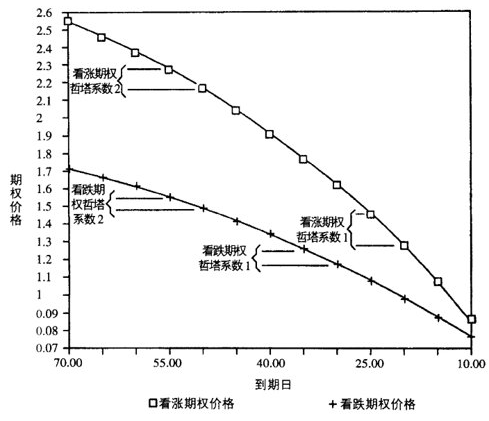
- For options with the same maturity, ATM options have the largest absolute Theta value; the closer to expiration, the larger the absolute Theta value.
- When the option has a long time to expiration, Theta is very small; it increases rapidly as expiration approaches.
Vega – Change in Volatility
Vega : Measures how the option premium of the underlying asset is affected by changes in volatility (σ). It is expressed as the amount of money the option gains or loses when volatility increases or decreases by 1%. Vega is particularly important in volatile markets for monitoring an option's premium.
- Buy Vanilla option (call/put) → Vega is positive.
- Sell Vanilla option (call/put) → Vega is negative.
Rho – Sensitivity to Interest Rate Changes
Rho : Measures the sensitivity of the option premium to changes in interest rates (r).
- For call options, rho is positive; for put options, rho is negative. In other words, when interest rates rise, call option prices increase, while put option prices decrease.
- We consider buying a call option as an alternative to buying the stock. Buying stock requires capital, but buying a call option does not. The saved capital can generate interest income, so when interest rates are high, call option prices rise.
- Interest rates are considered the least important parameter in option pricing models.
Rho and Phi:
Rho measures the sensitivity of a portfolio's value to changes in interest rate levels. Generally, currency options have two Rhos: one for the domestic interest rate and another for the foreign currency interest rate. It measures the sensitivity of the portfolio value to interest rate changes. For call options, Rho is typically positive, while for put options, Rho is typically negative.
Rho represents the expected change in the option premium due to a small change in the domestic currency interest rate. Phi represents the expected change in the option premium due to a small change in the foreign currency interest rate.
Reference:
The Complete Guide to Option Pricing Formulas-Haug.pdf, P71
Black-Scholes Merton Greeks
Spot Delta
For example, consider a futures option with six months to expiration. The futures price is 105, the strike price is 100, the risk-free interest rate is 10% per annum, and the volatility is 36% per annum. Thus, .
Forward Delta
The interpretation of Forward Delta is how many units (FOR) of forward contracts a trader needs to buy to hedge a short option position:
Strike From Delta
In some over-the-counter (OTC) markets, options are quoted in terms of Delta rather than strike price. For example, in the OTC currency options market, it is common to ask for a Delta and expect the salesperson to return a price (in volatility or points) and the strike price given a spot reference. In these cases, it is necessary to find the strike price corresponding to a given Delta. Many option software systems solve this numerically using Newton-Raphson or bisection methods. However, this is not actually necessary. The strike price can be derived analytically from the Delta by inverting the cumulative normal distribution function , as described by Wystrup (1999). For a call option:
For a put option:
For example, to achieve a Delta of 0.25 for a three-month stock index call option, assume the risk-free rate is 7%, the dividend yield is 3%, volatility is 50%, and the stock index is trading at 1800. Given parameters: .
Calculation yields:
Then, the strike price can be calculated using:
Thus, to achieve a Delta of 0.25, the strike price should be set to 2217.0587.
Gamma
Gamma is the sensitivity of Delta to small changes in the underlying asset price. Gamma is the same for calls and puts:
This is the standard gamma measure given in most textbooks (like Hull (2005) and Wilmott (2000)). It measures the change in Delta for a unit change in the underlying asset price.
For example, consider a stock option with nine months to expiration. The stock price is 55, the strike price is 60, the risk-free interest rate is 10% per annum, and the volatility is 30% per annum. .
Vega
Vega is the sensitivity of the option to small changes in the volatility of the underlying asset. Vega is the same for calls and puts.
For example, consider a stock index option with nine months to expiration. The index price is 55, the strike price is 60, the risk-free interest rate is 10.50% per annum, the dividend yield is 3.55% per annum, and the volatility is 30% per annum. What is the Vega? , , the calculated Vega value is:
To convert this to Vega for a one percent change in volatility, we need to divide Vega by 100. Thus, if volatility changes from 30% to 31%, the option value will increase by approximately 0.1850.
Theta
Theta is the sensitivity of the option to small changes in time to expiration. As time to expiration decreases, it is common to express Theta as the negative partial derivative with respect to time.
Call
Put
Consider a European put option on a stock index currently priced at 430. The strike price is 405, time to expiration is one month, the risk-free interest rate is 7% per annum, the dividend yield is 5% per annum, and the volatility is 20% per annum. , the calculation yields:
Therefore, the daily time decay Theta value is -31.1924/365=-0.0855.
Rho
Rho is the sensitivity of the option to small changes in the risk-free interest rate.
Call
Put
For example, consider a European call option where the underlying asset is currently priced at 72. The strike price is 75, time to expiration is one year, the risk-free interest rate is 9% per annum, and the volatility is 19% per annum. Thus, ,
If the risk-free interest rate changes from 9% to 10%, the call option price will increase by approximately 0.3873.
Vanna
Vanna is sometimes called dvega/dspot. It reflects how the Vega value changes as the underlying asset price changes. A trader's Vanna assumes a 1% relative change in the underlying asset price. The origin of the term Vanna is unclear. I suspect it can be traced back to an article in the 1990s in Risk magazine by Tim Owens, who asked, "Want to lose a lot of money?" and then explained how losses could occur if second-order Greeks like Vanna and Volga are not hedged.
Volga
Volga is sometimes called vomma or volgamma or dvega/dvol. Volga reflects how the Vega value changes as volatility changes. A trader's Volga assumes a 1% absolute change in volatility.
Numerical Greeks (Sensitivity Calculation using Numerical Methods)
So far, we have only looked at Analytical Greeks. A frequently used alternative is to use Numerical Greeks, also known as Finite Difference Approximations. The main advantage of Numerical Greeks is that their calculation is independent of the model considered. As long as we have an accurate model to calculate the value of the derivative, the finite difference approximation will give us the Greek values we need.
First-Order Greeks
The first-order partial derivative can be approximated by the central finite difference method:
For the derivative with respect to time, we know the direction of time's movement, and using a backward derivative (one-sided finite difference) is more accurate (for what happens in the "real" world). That is:
Numerical Greeks have several advantages over analytical Greeks. For example, if we have a sticky delta volatility smile, we can correspondingly change the volatility when calculating the numerical Delta. (When the volatility curve moves with changes in the underlying asset price, we call it a sticky delta volatility curve; in other words, the volatility for a given strike price moves with changes in the underlying asset price.)
Furthermore, numerical Greeks are model-independent, whereas the analytical Greeks above are specific to the BSM model.
Second-Order Greeks
For speed and other third-order derivatives , we can use the following approximation:
Mixed Greeks
For mixed derivatives , for example
DdeltaDvol and charm can be obtained through numerical calculation. For DdeltaDvol, it is usually divided by 100 to get the "correct" representation, i.e., for a one-point change in volatility.
Third-Order Mixed Greeks
For Greeks like DgammaDvol, we need to calculate third-order mixed Greeks :
For DgammaDvol, it is also usually divided by 100 to get the "correct" representation.
Calculating Delta using Numerical Methods
raw delta = (v₁ – v₂) / (2 × bump)
Here:
raw delta
- Calculated by the finite difference method:
raw delta = (v₁ – v₂) / (2 × bump) - Here v₁ and v₂ are the option prices after bumping up and down respectively, and bump is the unit change in spot.
- Calculated by the finite difference method:
premium adjusted delta
- Takes into account the effect of the option premium on sensitivity.
- For FX options, it usually requires deducting the ratio of the option price relative to the spot.
ccy2 delta
- Generally refers to the delta denominated in the foreign currency.
- Defined as:
ccy2 delta = raw delta
ccy1 delta
- Refers to the delta denominated in the domestic currency, expressed as:
ccy1 delta = raw delta – v₀/S - Where v₀ is the option price and S is the current spot exchange rate.
- Refers to the delta denominated in the domestic currency, expressed as:
How to Calculate Forward Delta for American Options?
Some option pricing models, such as the BAW or PDE models for American options, do not have forward as an input parameter in their calculation models, so forward delta cannot be calculated directly by changing the forward.
Below is a common method to obtain the forward delta for FX American options using bump and reprice. The key is to recognize:
Forward = S × exp[(r_d – r_f) × (T – t)]
If your pricing program only provides S, r_d, and r_f, then forward is not passed as a separate input parameter, but it can be calculated based on the above formula.
1. Basic Idea
Suppose you want to calculate the forward delta, i.e., the sensitivity of the option price to the forward, denoted as
Δ_F = ∂V/∂F
Since the relationship between forward and spot is
F = S × exp[(r_d – r_f) × (T – t)]
using the chain rule we have
Δ_F = (∂V/∂S) × (∂S/∂F)
= Δ_S / exp[(r_d – r_f) × (T – t)]
where Δ_S = ∂V/∂S is the traditional spot delta.
2. Bump and Reprice Calculation Method
Using the bump and reprice method, you can proceed as follows:
Calculate the base price
Price the option using the current S, r_d, r_f to get the option price V(S).Determine the bump size
Suppose you want to bump the forward by ΔF. As mentioned earlier, due to the relationship between F and S
ΔF = exp[(r_d – r_f) × (T – t)] × ΔS
Therefore, to bump the forward by ΔF, you need to increase S by
ΔS = ΔF / exp[(r_d – r_f) × (T – t)]Calculate the bumped price
Let the new spot be S_bumped = S + ΔS, then rerun the FDM model with the new spot to get the bumped price V(S_bumped).Calculate the spot delta
Δ_S ≈ [V(S_bumped) – V(S)] / ΔSConvert to forward delta
According to the chain rule, the forward delta is
Δ_F ≈ Δ_S / exp[(r_d – r_f) × (T – t)]
Or equivalently, directly using the price change from bumping the forward:
Δ_F ≈ [V(S_bumped) – V(S)] / ΔF
The two methods are consistent under the conversion relationship between ΔS and ΔF. The key is that the bump must correspond to a change in the forward, not simply an absolute bump to S.
Special Considerations for FX Options
In foreign exchange options, similar to Volga, Delta, Gamma, Vega, Vanna, Theta, Rho and other Greek values (collectively "Greeks") often exhibit numerical inconsistencies or even differences by factors of 100 due to variations in units and measurement methods. Below is a general summary to help understand the common representations and meanings of these indicators in FX options.
1. Common Sources of "Unit Differences"
Note: In practice, different systems may show consistent numbers but differ by a factor of 100. In such cases, we need to pay attention to the units of these Greek letters. Different systems may have different final display units for these systems!
1) Differences in Measurement Level
- Percentage (%): A measure is conducted in "percentage" form, such as "a 1% change in volatility" or "a 1% change in the underlying exchange rate." In numerical calculations, 1% is often converted to the decimal 0.01.
- Basis Points (bps): If the system is accustomed to measuring in basis points, then 1 basis point (bp) = 0.0001 (i.e., 0.01%), and 1bp may need to be converted to 0.0001.
- Absolute Amount: If the system measures in "absolute currency units" (e.g., a change in the underlying exchange rate from 1.1000 to 1.1001 counts as 1 pip), then the dimensions of Delta, Vega, etc., will differ from those measured in percentages.
2) Differences in Exchange Rate Conversion
- FX options often involve two currencies: the Base Currency and the Quote Currency. For example, in EUR/USD, EUR is the base, USD is the quote.
- Delta may sometimes be given as Delta in the base currency (often called the foreign currency), and may sometimes be converted to Delta in the pricing currency (domestic currency).
- Some systems (like Reuters, Bloomberg, Murex) provide multiple fields or different display methods for the same Greek value corresponding to different measurement methods.
2. Major Greeks and Their Common Units
Below lists the more common Greek indicators in FX options and explains the possible "unit" forms they may appear in.
2.1 Delta
- Definition: Delta represents the change in the option price for a small change in the underlying exchange rate (or underlying price).
- Unit Differences:
- EUR (Base Currency) or USD (Quote Currency): For example, how much USD the value of a "10,000 EUR contract" changes when the underlying exchange rate moves by 0.0001. It could also be the value change for a change of 1 in the underlying exchange rate.
- %: It could also be how much the option value changes "when the underlying exchange rate changes by 1%"; or how the value changes "when volatility changes by 1%" (though the latter is more commonly used for Vega).
- Some systems may present it as Spot Delta / Forward Delta; some also distinguish between Domestic Currency Delta / Foreign Currency Delta.
Example: If you see "Delta = 0.45 (EUR%)", it usually means:
When the underlying EUR/USD exchange rate increases by 1% (i.e., the exchange rate × 1.01), the value of this option will increase by approximately 0.45 euros (or as a percentage of the contract notional); the specifics depend on how the system defines the notional amount.
2.2 Gamma
- Definition: Gamma represents the change in Delta when the underlying exchange rate changes.
- Unit Differences: Common ones include
- How much the option value changes "per 1 (absolute) change in the underlying exchange rate";
- The second-order change in the option value "per 1% or 1bp change in the underlying exchange rate";
- In the FX field, there may also be markings like "% per %".
- Also involves base currency and quote currency: e.g., "Gamma(USD)" vs "Gamma(EUR)".
2.3 Vega (or Kappa)
- Definition: Vega represents the change in the option value for a small change in volatility.
- Unit Differences:
- Sensitivity to a 1% change in volatility: Commonly marked as "USD per % vol" or "EUR per % vol".
- Sensitivity to a 1bp (0.0001 = 0.01%) change in volatility: Some systems express it as "USD per 1bp", in which case the numerical value will be 100 times larger than the former.
- In FX, the sensitivity to volatility for Vega, Volga, Vanna, etc., may also be specified whether it is from the perspective of atm volatility or local volatility, and whether it is from domestic vol or foreign vol.
2.4 Volga (or Vomma)
- Definition: Volga, also known as Vomma, represents the sensitivity of Vega to changes in volatility.
- Unit Differences: Similarly, it could be the change in Vega (or the second-order effect on the option value) "for a 1% or 1bp change in volatility".
- If your system uses "/100", it means it converts 1% → 0.01; if you want to align with a system that measures in "basis points", you may need to use "/10000".
2.5 Vanna
- Definition: Vanna represents the change in the option value when both the underlying exchange rate and volatility change simultaneously (or the change in Delta with respect to volatility, or the change in Vega with respect to the underlying asset).
- Unit Differences: It is also often divided into sensitivity "for a 1% change in the underlying exchange rate and a 1% change in volatility" or "a 1bp change in the underlying exchange rate and a 1bp change in volatility".
2.6 Theta
- Definition: Theta represents the change in the option value over a small period of time (usually 1 day).
- Unit Differences:
- "USD per day" or "EUR per day";
- Some are annualized and then divided by the number of days, leading to an order of magnitude difference;
- Some systems express it as "the option value decreases by (-0.xx) dollars per day passed".
2.7 Rho
- Definition: Rho represents the change in the option value for a small change in interest rates.
- Unit Differences:
- "Dollars per 1% change in interest rate"
- "Dollars per 1bp (0.01%) change in interest rate"
3. How to Distinguish Different Greek Value Units?
- Look at the field descriptions provided by the system
- For example, Bloomberg's
VEGAfield is usually in "$ per 1 vol%", but some places may additionally provide a "$ per 1bp" version. - Reuters / Murex will also have corresponding annotations, or indicate behind the field something like
(BS pips/Vol%).
- For example, Bloomberg's
- Check the numerical magnitude
- If you find that your calculation is 100 times larger or smaller than the other party's, it is likely the difference between "% vs. bps" or "/100 vs. /10000".
- Compare against the notional currency
- The difference between "Delta(EUR)" vs. "Delta(USD)" is often just a multiplication or division by the exchange rate in between.
4. Summary
- Various Greeks indicators (Delta, Gamma, Vega, Volga, Vanna, Theta, Rho, etc.) in FX options all have distinctions in "units" and "base currency".
- The difference between "/100" and "/10000" is essentially the difference between "a measured 1%" (i.e., 0.01) and "a measured 1bp" (i.e., 0.0001).
- "EUR%" and "USD%" often represent the change in the option value in the corresponding currency for a 1% (or 1bp) change in the EUR/USD exchange rate; they could also be absolute currency amounts ("EUR amount" / "USD amount").
- There is no unified "standard": The key is to understand the "numerical units" and "currency basis" conventions for each Greek value in the system or platform you are using (Bloomberg, Reuters, Murex, in-house systems, etc.), and ensure consistency when comparing or interfacing.
In a nutshell:
If you are comparing numerical values with an external system and encounter differences of 100 times or 10,000 times, first check: "Is it using % (/100) or bps (/10000)? Is it using the base currency or the quote currency? Is it necessary to multiply/divide by an exchange rate conversion?"
Once you clarify these issues, you can accurately align the units of each Greek value.
3. Summary
- Due to the relationship between FX forward and spot, F = S × exp[(r_d – r_f)(T – t)], when you want to calculate the forward delta using bump and reprice, you can calculate the corresponding spot bump based on the forward bump.
- The specific method is: set the forward bump ΔF, calculate the corresponding ΔS, re-price to obtain V(S_bumped), thereby obtaining the spot delta, and then divide by exp[(r_d – r_f)(T – t)] to get the forward delta.
- You can also directly write the bump value in terms of price change as:
Δ_F ≈ [V(S + ΔS) – V(S)] / ΔF
This way, even if the forward is not explicitly passed as a parameter in the program, the forward delta can be derived through the spot bumping process.
Visit the Mathema Option Pricing System for more FX option pricing tools and resources
