SOFR Curve Construction Methodology: Instruments, Process, and Practice

1. Core Construction Instruments and Market Conventions

Constructing the SOFR curve primarily relies on the following market instruments. Understanding their conventions and pricing formulas is crucial:

1. SOFR and SOFR Index:

   • SOFR: The overnight rate published daily by the Federal Reserve Bank of New York.
   • SOFR Index: A cumulative index reflecting the value of $1 compounded daily at SOFR since a base date. The calculation formula is: Index_T = Index_0 * ∏(1 + SOFR_i * d_i/360). It is the gold standard for calculating accrued interest.

2. SOFR Futures:

   • 1-Month SOFR Futures (SR1): Its price 100 - SR1 represents the simple average of all daily SOFR forward rates within the contract month. The pricing formula is as follows:

     $$100-SR1\approx\frac{1}{N_{m}}\sum_{i=1}^{N_{m}}SOFR^{Fwd}_{t_{i}}$$

     where $N_{m}$ represents the number of days in the contract month, and $t_{i}$ represents the time corresponding to the contract reset dates. It trades the expectation of the future average overnight rate.
   • 3-Month SOFR Futures (SR3): Its price 100 - SR3 represents the annualized result of the overnight rate compounded daily over a contract quarter. The pricing formula is as follows:

     $$100-SR3\approx\frac{360}{N_{Q}}\left(\prod_{i=1}^{Q}\left(SOFR^{Fwd}_{t_{i}} \frac{dt_{i}}{360}+1\right)-1\right)$$

     where $N_{Q}$ is the number of days in the reference quarter, and $dt_{i}=t_{i+1}-t_{i}$ is the tenor of the forward rate (which may not be 1 day due to holidays). It trades the expectation of the future compounded overnight rate.
   • Key Feature: Futures continue trading after the reference period begins. Therefore, the pricing formula must mix realized rates(SOFR^{Rzd}), pre-bootstrapped rates(SOFR^{Btd}), and unknown forward rates(SOFR^{Fwd}). For example, for current time t, the complete formula for SR1 is:

     $$100-SR_{1}=\frac{1}{N_{m}}\sum_{i=1}^{N_{m}}(SOFR^{Rzd}_{t_{i}<t}+SOFR^{Fwd}_{t_ {i}\geq t})$$

3. SOFR Swaps:

   • A swap where a fixed rate is exchanged for a floating rate, where the floating leg is SOFR compounded over the payment period.
   • Unlike LIBOR swaps which use OIS for discounting, SOFR swaps use the SOFR curve for dual curve discounting and forecasting.
   • For a par swap starting at T₀ and maturing at T, the fixed rate K is the solution to the following equation:

     $$\sum_{j}\left(\prod_{i}\left(1+SOFR_{T_{j-1}<t_{i}\leq T_{j}}\frac{dt_{i}}{360 }\right)-1\right)\frac{360}{dT_{j}}P(0,T_{j})=\sum_{j}KP(0,T_{j})$$

     where $SOFR_{T_{j-1}<t_{i}\leq T_{j}}$ represents all bootstrapped and forward SOFR rates within year j, and $P(0,T_j)$ is the discount factor for maturity T_j.

2. Standard Construction Process: Layered Bootstrapping Method

The standard construction method aims to create an arbitrage-free forward curve. Its core is the sequential use of different instruments to solve for forward rates step by step from short to long end. The process is as follows:

Step 1: Determine the Spot Rate (Spot SOFR)

• Use the latest SOFR spot rate published by the NY Fed as the starting point of the curve. For example, a spot rate of 0.04% implies a theoretical price of 99.96 for the front SR1 future (SR1-0).

Step 2: Bootstrap the Short-End Curve - SOFR Futures (SR1 & SR3)

• Handling the Front Contract: For SR1/SR3 contracts that are about to expire or have entered their reference period, their prices include realized SOFR rates. These known components must be stripped out from the quotes, solving only for the forward rates on the remaining unknown dates. For example, the complete bootstrapping formula for SR3 needs to consider three types of rates:

$$1-SR_{3}=\frac{360}{N_{Q}}\left(\prod_{i=1}^{Q}\left(SOFR^{Rzd}_{t_{i}<t}\frac {dt_{i}}{360}+1\right)\prod_{i=1}^{Q}\left(SOFR^{Btd}_{t\leq t_{i}<t^{\prime}} \frac{dt_{i}}{360}+1\right)\prod_{i=1}^{Q}\left(SOFR^{Fwd}_{t_{i}\geq t^{\prime }}\frac{dt_{i}}{360}+1\right)-1\right)$$

• Constant Forward Assumption: Between adjacent futures contracts, it is common to assume forward rates are constant. Using the bootstrapping method, solve for each segment of forward rates sequentially so that the theoretical price of each future calculated from the curve minimizes the difference from its market quote.
• Instrument Sequence and Overlap Handling: Prefer shorter-term SR1 futures first, as they provide finer interest rate signals. The rates for the portion where the SR3 contract overlaps with SR1 ($SOFR^{Btd}$) are already determined by SR1. SR3 is then used to bootstrap the rates for its remaining portion ($SOFR^{Fwd}_{t_i \geq t'}$).

Step 3: Bootstrap the Medium to Long-End Curve - SOFR Swaps (SWAPs)

• On the basis of the short-end curve (built from futures), introduce liquid par swap quotes.
• Bootstrapping Process: Start with the shortest maturity swap (e.g., 2-year) and ensure its Net Present Value (NPV) is zero. For early-term swaps, cash flows for some years may already be determined by the futures curve (i.e., "pre-bootstrapped"). The optimizer adjusts the unknown forward rates so that the present value of these known cash flows plus the present value of the unknown cash flows equals the present value of the fixed leg, thus making the entire swap NPV zero.
• In a simplified scenario ignoring holidays, the annualized swap pricing formula can be written as:

  $$\sum_{j}\left(\left(1+SOFR_{T_{j-1}<t_{i}\leq T_{j}}\frac{1}{360}\right)^{365}-1 \right)\frac{360}{365}P(0,T_{j})=K\sum_{j}P(0,T_{j})$$

3. Model Validation: Comparative Analysis of MCP Self-Built Curve vs. Bloomberg CURV System

To validate the accuracy and reliability of the self-built SOFR curve model, we used the Mammoth Calculation Plus (MCP) Excel template to construct a SOFR curve and conducted a comprehensive comparison with the standard SOFR curve in the Bloomberg Terminal's CURV system. The input data required for construction (SOFR spot rate and SOFR swap rates) were directly obtained from the Bloomberg Terminal, ensuring consistency in the comparison basis.

Input Data for SOFR Curve in Bloomberg's CURV Module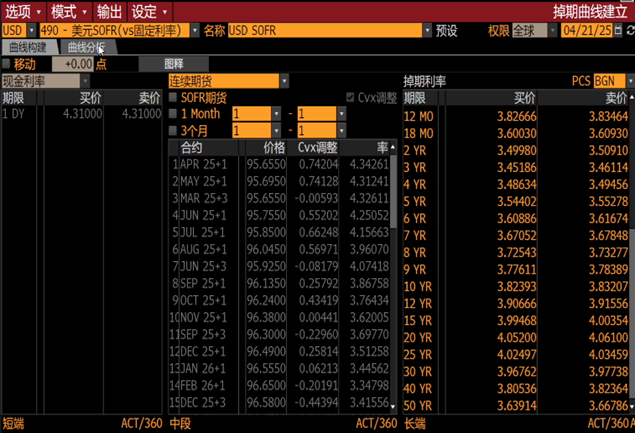

Spot and Discount Analysis of SOFR Curve in Bloomberg's CURV Module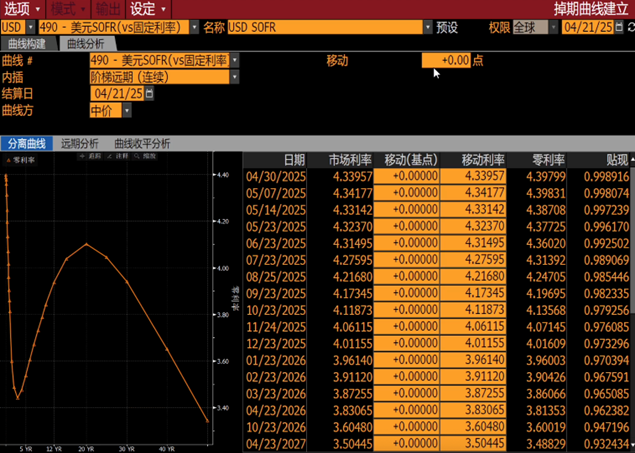

MCP Excel Curve Construction

📊 Click to Download Excel Template (MCP SOFR Curve(BBG).xlsx)
❓ Download and Install MCP Excel Package

MCP Excel Curve Analysis and Comparison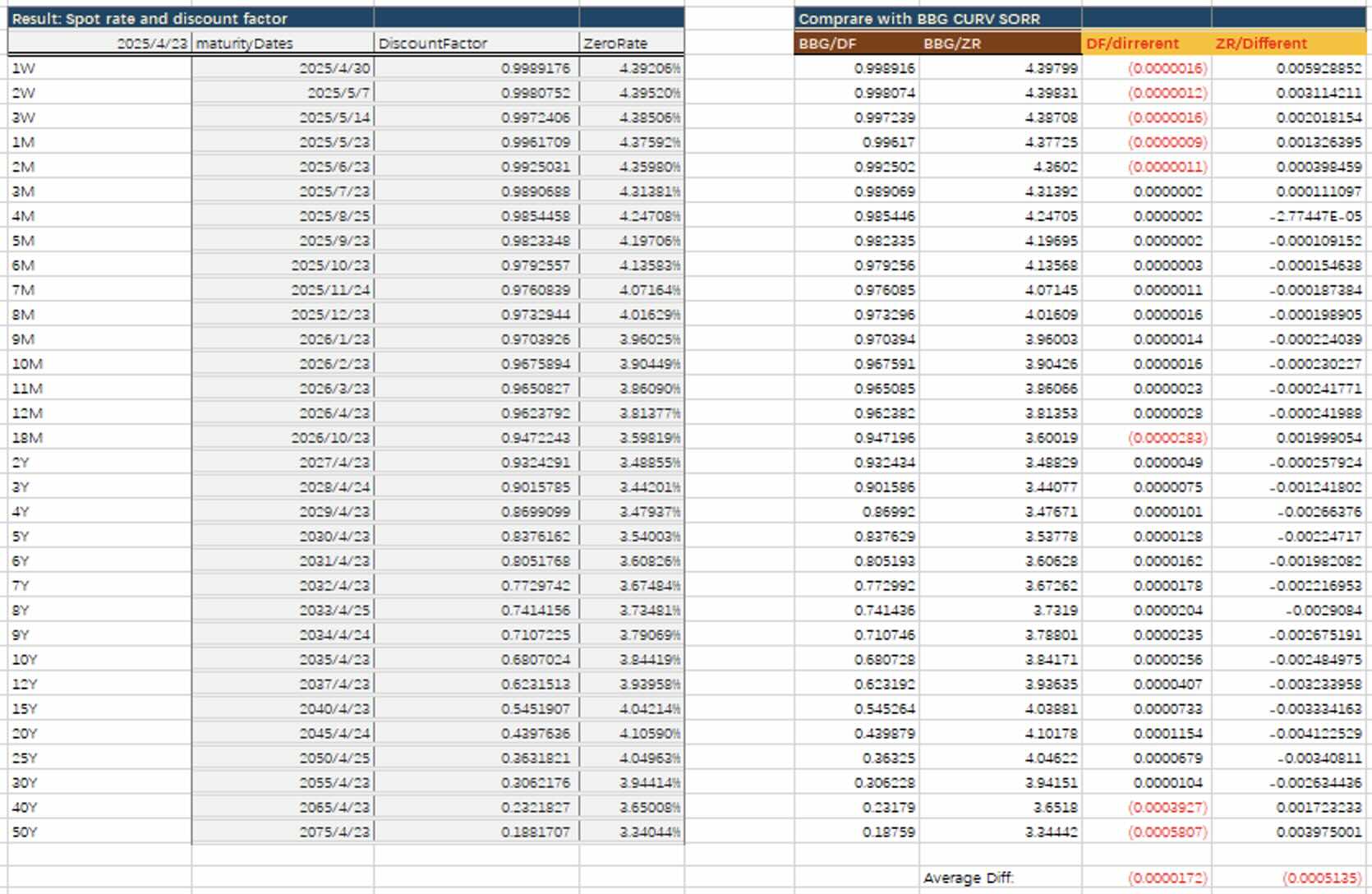

Comparison Results and Conclusions:

1. High Precision: The comparison results show a high degree of consistency between the self-built curve and the Bloomberg curve in terms of Discount Factors (DF) and Zero Rates (ZR). The differences in discount factors for the vast majority of maturity points are within 0.00002, and the differences in zero rates are within 2.5 basis points (0.0025%). The average differences are only -0.0000172 and -0.0005135% respectively. This indicates that the core logic of the self-built bootstrapping algorithm is correct, successfully replicating the pricing results of the market standard curve.
2. Very High Short-Term Precision: For shorter maturities (within 2 years), the differences are minimal. Discount factor differences are essentially less than 0.000003, and zero rate differences are mostly less than 0.002%. This proves the model's extremely high accuracy for the start of the curve and cash instrument pricing.
3. Excellent Medium to Long-Term Performance: For longer maturities (2 to 30 years), the differences remain very low. Although the differences widen slightly at个别点 (e.g., 40Y, 50Y), this is due to relatively poorer liquidity in ultra-long tenors, sparse quote points, and potential slight differences in interpolation methods, which is normal. Overall, the self-built curve is equally reliable for pricing medium to long-term swaps.
4. Practical Significance: This validation result fully demonstrates that, based on a clear bootstrapping methodology and reliable market data, it is entirely possible to independently construct a SOFR curve aligned with industry standards outside of the Bloomberg Terminal (e.g., using Mammoth Options Excel or other quantitative platforms). This provides a feasible alternative for users who cannot directly access the Bloomberg Terminal and offers important benchmark verification basis for model risk control.

4. Methodology Choice: Futures + Swaps vs Index + Swaps

There is not just one absolutely "correct" method for building a SOFR curve; the choice highly depends on the ultimate purpose of the curve.

Characteristic	Method 1: Futures + Swaps (For Derivatives Pricing)	Method 2: Index + Swaps (For Cash Asset Valuation)
Core Purpose	Forecast the future for pricing derivatives	Calculate the past for valuing cash assets and discounting
Time Orientation	Forward-Looking	Backward-Looking + Current Discounting
Core Inputs	SOFR Futures (short end) + SOFR Swaps (long end)	SOFR Index (calculate interest) + SOFR Swaps (provide discount rate)
Methodology	Arbitrage-Free Bootstrapping, extracting forward rates	Index Division for interest calculation + Swap Curve for discounting
Key Outputs	Instantaneous Forward Rates	Accrued Interest, Asset Present Value
Reason for Choice	Must be consistent with tradable derivatives (futures, swaps) prices, otherwise arbitrage exists. The only choice for trading, hedging, and derivatives valuation.	Must be completely consistent with officially published historical actual data to ensure objectivity and accuracy of interest calculation. The ideal choice for accounting, asset valuation, and risk control.

• For Traders, Quantitative Analysts, and Derivatives Market Makers, it is necessary to use SOFR Futures + SOFR Swaps to build a refined, arbitrage-free forward curve. This curve can precisely calibrate market expectations for the future path of interest rates and is the cornerstone for pricing complex derivatives like options and swaps.
• For Asset Managers, Accountants, and Risk Officers, the core task is to accurately calculate the accrued interest and fair value of held assets. In this case, the SOFR Index + SOFR Swaps curve is a more appropriate choice. It uses the SOFR Index to perfectly look back at history (Interest = Principal * (Index_B / Index_A - 1)), and uses the swap curve to provide a market-based discount rate, ensuring the objectivity and auditability of valuation results.

References

1. Abramov, V., Zhou, X., & Zhengye, B. (2020). SOFR Bootstrapping Modeling Methodologies and Issues (w/ Python and Excel Replicas of Bloomberg SOFR @ GitHub). SSRN. https://ssrn.com/abstract=3654466

   • This paper discusses in detail the modeling methods and issues of SOFR bootstrapping, as well as the differences from traditional Libor bootstrapping. It provides Python and Excel implementation examples and is an important technical document for understanding the practice of SOFR curve construction.

2. CME Group. (2020, May 13). SOFR Futures Celebrate Two-Year Anniversary. Retrieved from CME Group Newsroom.

   • Provides key data on the development history and trading volume of the SOFR futures market, illustrating its growth in liquidity and market acceptance.

3. CME Group. (2018, Q4). OTC SOFR Swaps Clearing. CME Group Clearing Documentation.

   • Outlines the clearing specifications for over-the-counter (OTC) SOFR swaps, including their contract specifications. It is a fundamental document for understanding the mechanics of SOFR swaps.