Practical Implementation and Modeling of Swaption Cube Construction

1. Swaption Cube

In interest rate derivatives trading and risk management, the Swaption Cube serves as a core pricing/hedging tool. It organizes implied volatilities across different expiries (Expiry), strike rates (Strike), and swap tenors (Swap Tenor) into a three-dimensional grid, enabling rapid pricing and sensitivity analysis for any swaption combination.

2. Swaption Explained

• A Swaption grants the buyer (or seller) the right to enter (or exit) an interest rate swap (IRS) at a future date.
• The key parameter for counterparties is the implied volatility, which reflects market expectations of future rate volatility.
• However, derivatives trading often spans multiple expiries and swap tenors (e.g., 2Y→5Y, 5Y→10Y, 10Y→30Y).
• A single ATM curve can no longer cover all requirements, necessitating construction of a complete surface including non-ATM strikes, which is then combined into a cube to support cross-tenor pricing and risk management.

3. Market Data and Quotation Formats

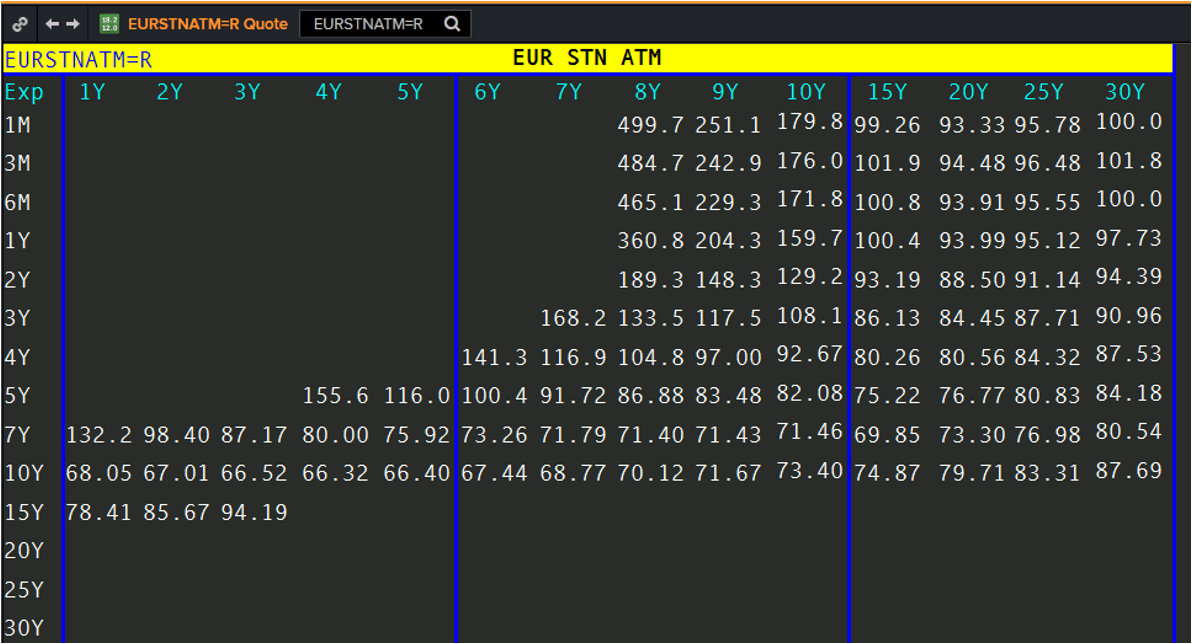
3.1 ATM Quotations

The most common swaption quotes are ATM Volatilities:

• Period: Swaption expiry (e.g., 1Y, 2Y...)
• Strike: ATM strike for the given expiry—typically the current par swap rate.
• Vol: Annualized implied volatility for this strike.

Below is an example of Refinitiv's ATM EUR Vol:

image-20250630104547584

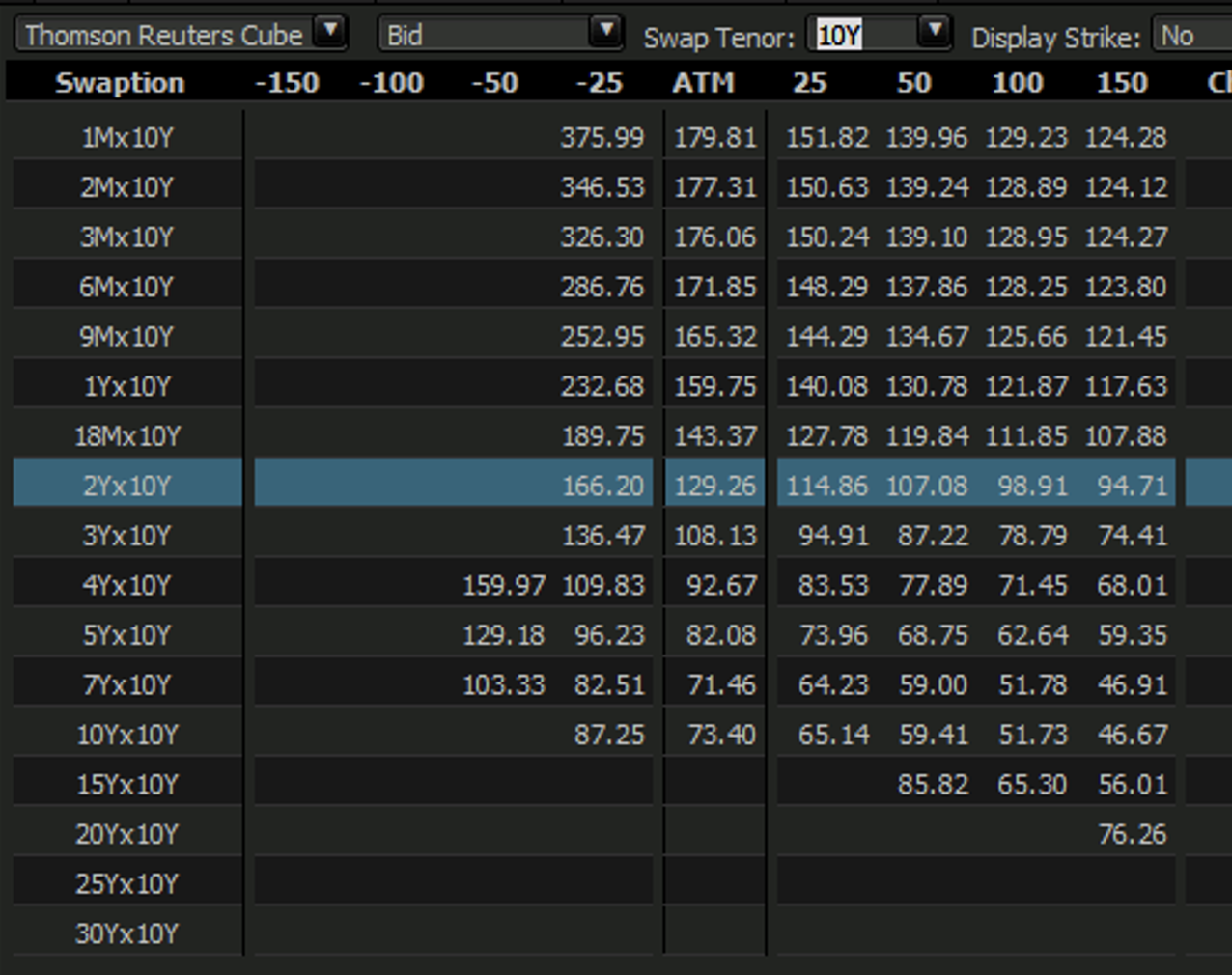
3.2 Non-ATM Quotations

Beyond ATM, some markets also provide:

• Risk-Reversal (RR) and Butterfly (BF): Reflecting OTM call/put skew/butterfly.
• OTM Vols: Direct quotes of implied volatilities at specific strikes deviating from ATM.

If only ATM data is available, parametric models (e.g., SABR) or specific interpolation assumptions must be employed to "fill" the entire strike dimension.

Below is an example of Refinitiv's non-ATM Vol:

image-20250630104700161

4. Normal Vol vs. Black Vol

In interest rate option pricing, two primary volatility measures exist:

	Bachelier Model (Normal Vol)	Black-76 Model (Black Vol)
Definition	Absolute volatility: $\sigma_n$ (in bp)	Relative volatility: $\sigma_b$ (%)
Formula	$C = N\bigl((F-K)/(\sigma_n\sqrt{T})\bigr)\times\sigma_n\sqrt{T}$	Classic Black-76: $C = B\,N(d_1) – K\,B\,N(d_2)$
Use Case	Low-rate/negative rate environments	Traditional positive-rate environments
Conversion	Requires numerical solution: Normal-Price ⇄ Black-Price σ mapping	Near ATM: $\sigma_b\approx\sigma_n/F$

In the post-crisis low-rate environment, Normal Vol has gained prominence. However, many legacy models (e.g., Black-76, SABR) are log-normal by design, necessitating flexible conversion between measures.

Note: MCP pricing systems also use:

• Price‐Vol (Normal Vol, Bachelier)
• Yield‐Vol (Log-Normal Vol, Black-76)

For details: Normal vs. Log-Normal Volatility

5. Swaption Cube Construction Workflow

Below is a standard workflow from market ATM quotes → parametric modeling → 3D interpolated cube.

5.1 Data Preparation

1. Collect ATM Curves

   • Expiries $\{T_i\}$: e.g., 1Y, 2Y, 3Y...30Y.
   • ATM strikes $\{K_i\}$: Corresponding par swap rates or swaption ATM strikes.
   • ATM volatilities $\{\sigma_i\}$: Normal/Black convention.

2. (Optional) Collect OTM Skew Data

   • RR/BF or vols at selected in/out strikes.

3. Define Swap Tenor Structure

   • Common tenors: 1Y, 2Y, 5Y, 10Y...30Y.

5.2 Model Selection

5.2.1 Parametric Skew: SABR

The standard approach calibrates a three-parameter SABR for each $(T_i,\text{SwapTenor}_j)$ pair:

$$\{\alpha_{ij},\;\rho_{ij},\;\nu_{ij}\}$$

• Solve for $\alpha$ using ATM vol;
• If skew data exists, fit $\rho,\nu$ via least squares;
• Otherwise, interpolate $\rho,\nu$ smoothly or use historical estimates.

With SABR parameters per node, Hagan's formula outputs $\sigma_{ij}(K)$ for any strike $K$.

5.2.2 Non-Parametric Interpolation

If sufficient OTM vol points exist, apply 1D interpolation (linear, spline, etc.) directly along the strike dimension without modeling assumptions.

5.3 3D Interpolation Architecture

1. Strike Dimension

   • For each $(T_i,\text{SwapTenor}_j)$, generate a vol vs. strike curve using SABR or 1D interpolation.

2. Expiry Dimension

   • For fixed swap tenors, interpolate vol curves across $\{T_i\}$ to form a Vol Surface.

3. Swap Tenor Dimension

   • Across $\{\text{SwapTenor}_j\}$, interpolate at fixed $(T,K)$ to complete the Swaption Cube.

This process can be implemented via sequential 1D interpolations/extrapolations or specialized 3D methods (trilinear, spline, Kriging, etc.).