正态与对数正态波动率 (NORMAL VS LOG-NORMAL VOLATILITY)

关于波动率的度量，有两种常见的方法：正态波动率（normal volatility）和对数正态波动率（lognormal volatility）

访问猛犸期权定价系统，支持外汇期权和结构化产品定价估值！

一、引言：两种波动率范式的起源与意义

在金融衍生品定价和风险管理领域，波动率的刻画方式从根本上决定了模型的行为特征。历史上有两种主要的波动率描述范式并行发展：

1. 正态（Bachelier）波动率：由Louis Bachelier在1900年提出，采用价格绝对变化的标准差度量，适用于算术布朗运动
2. 对数正态（Black-Scholes）波动率：由Black、Scholes和Merton在1973年完善，基于价格对数收益率的标准差，对应几何布朗运动

这两种看似简单的差异，导致了模型在数学性质、市场适用性和风险管理方面的深刻区别。本文将系统性地解析它们的理论基础、计算方法、转换关系及实务应用。

二、数学本质与核心公式

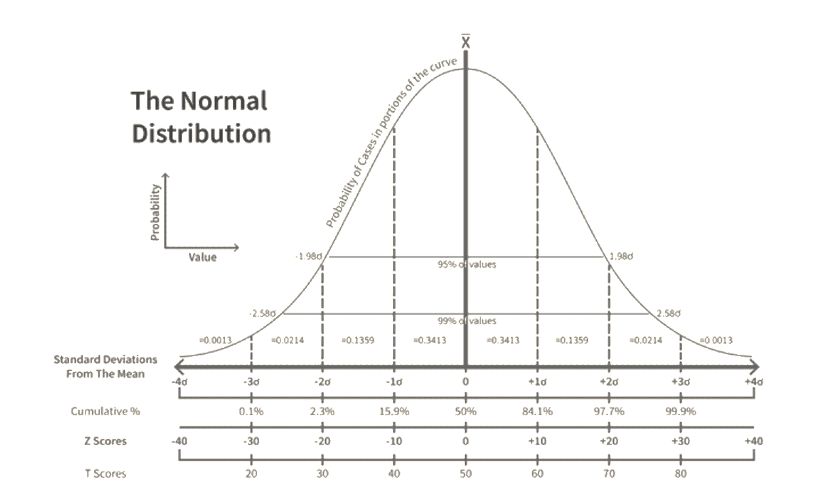
1. 正态波动率（σₙ）

定义：价格绝对变化的年化标准差
随机过程：

$$dS_t = \sigma_n dW_t$$

离散形式：

$$S_{t+\Delta t} = S_t + \sigma_n \sqrt{\Delta t} Z, \quad Z \sim N(0,1)$$

性质：

• 价格变化ΔS服从正态分布N(0, σₙ²Δt)
• 允许价格为负
• 波动率单位与价格相同（如美元/年）

image-20250617100754507

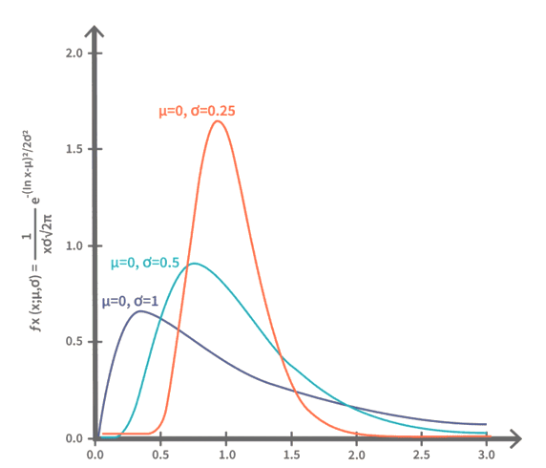
2. 对数正态波动率（σₗₙ）

定义：对数收益率的年化标准差
随机过程：

$$d\ln S_t = \left(\mu - \frac{1}{2}\sigma_{ln}^2\right)dt + \sigma_{ln} dW_t$$

离散形式：

$$S_{t+\Delta t} = S_t \exp\left[\left(\mu - \frac{1}{2}\sigma_{ln}^2\right)\Delta t + \sigma_{ln} \sqrt{\Delta t} Z\right]$$

性质：

• 对数收益率ln(Sₜ/S₀)服从正态分布
• 价格严格为正
• 波动率单位为百分比（如20%/年）

image-20250617100805668

3. 转换关系

在短期/小波动条件下：

$$\sigma_n \approx S_0 \times \sigma_{ln}$$

精确转换需考虑凸性调整：

$$\sigma_n = S_0 \sigma_{ln} \sqrt{T} \left(1 + \frac{1}{2}\sigma_{ln}^2 T \right)$$

4. 布朗运动与两种模型的关系

1. 布朗运动的数学基础

布朗运动（Brownian Motion，又称Wiener过程）是两种模型共同依赖的随机过程核心，定义为：

$$W_t \sim N(0, t)$$

性质：

• 独立增量：$W_{t+\Delta t} - W_t$与历史路径无关
• 正态分布：$\Delta W_t \sim N(0, \Delta t)$
• 路径连续但不可微

2. 在Bachelier模型中的应用

正态模型直接使用布朗运动的加性性质：

$$dS_t = \sigma_n dW_t$$

• 经济解释：价格变化$\Delta S_t$是布朗运动增量的线性缩放

• 离散形式：

$$S_{t+\Delta t} = S_t + \sigma_n \Delta W_t$$

• 分布特性：价格服从$N(S_0, \sigma_n^2 t)$，保留布朗运动的可负性

示例：
若$\sigma_n = 20$bps/√年，1天后价格变化标准差：

$$\sigma_n \sqrt{1/252} = 20 \times 0.063 \approx 1.26 \text{bps}$$

3. 在Black-Scholes模型中的变形

对数正态模型通过对数变换将乘性噪声引入布朗运动：

$$d\ln S_t = \left(\mu - \frac{1}{2}\sigma_{ln}^2\right)dt + \sigma_{ln} dW_t$$

• 经济解释：收益率$d\ln S_t$是漂移项与布朗运动的叠加

• 离散形式：

$$S_{t+\Delta t} = S_t \exp\left[(\mu-\frac{1}{2}\sigma_{ln}^2)\Delta t + \sigma_{ln} \Delta W_t\right]$$

• 分布特性：对数价格服从正态分布，保证$S_t > 0$

示例：
若$\sigma_{ln} = 20\%$，1天后收益率标准差：

$$\sigma_{ln} \sqrt{1/252} \approx 1.26\%$$

三、对应简单期权定价公式对比

1. 看涨期权定价

Bachelier（正态）模型：

$$C = (S_0 - K)\Phi(d) + \sigma_n \sqrt{T} \phi(d)$$

$$d = \frac{S_0 - K}{\sigma_n \sqrt{T}}$$

Black-Scholes（对数正态）模型：

$$C = S_0 \Phi(d_1) - K e^{-rT} \Phi(d_2)$$

$$d_1 = \frac{\ln(S_0/K) + (r + \sigma_{ln}^2/2)T}{\sigma_{ln} \sqrt{T}}$$

$$d_2 = d_1 - \sigma_{ln} \sqrt{T}$$

示例计算（S₀=100, K=105, T=1, r=0）：

• 正态：σₙ=20美元 → C≈7.12
• 对数正态：σₗₙ=20% → C≈6.89

2. 看跌期权定价

Bachelier模型：

$$P = (K - S_0)\Phi(-d) + \sigma_n \sqrt{T} \phi(d)$$

Black-Scholes模型：

$$P = K e^{-rT} \Phi(-d_2) - S_0 \Phi(-d_1)$$

四、市场报价形式实例

1. 外汇市场（对数正态惯例）

报价特点：

• 隐含波动率按Black-Scholes模型报价
• 波动率曲面以Delta为横坐标
• 标准格式示例：

期限	ATM	25D RR	25D BF
1M	11.2%	-0.5%	0.7%
1Y	10.5%	-1.2%	1.0%

其中：

• ATM：平值期权波动率
• RR（Risk Reversal）：看涨看跌波动率差
• BF（Butterfly）：波动率凸性调整

2. 利率市场（正态惯例）

利率上限/下限报价：

• 波动率通常按Bachelier模型报价
• 以基点(bps)为单位
• 市场数据示例：

image-20250617093449078

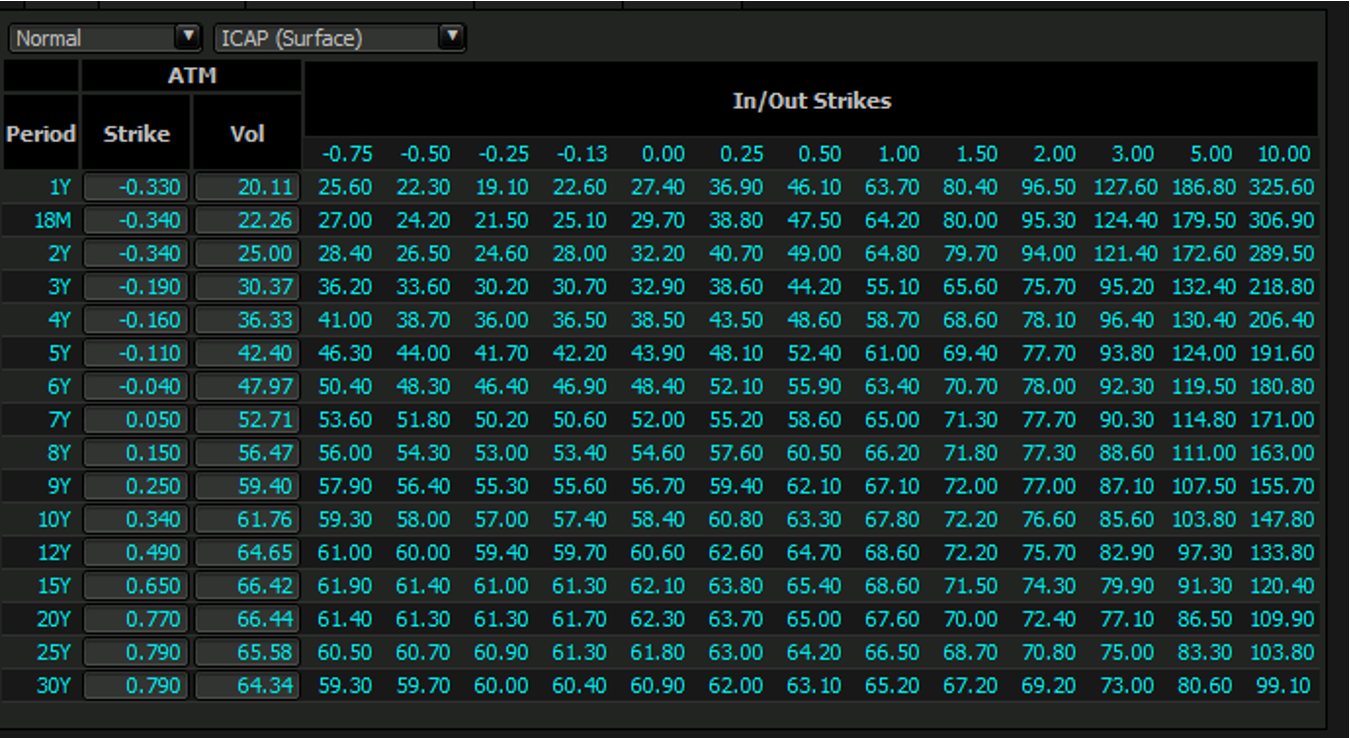
（1）列定义

列名	说明
Period	期权期限（1Y=1年期，30Y=30年期等）
Strike	平值期权的执行价（百分比表示，如-0.340%=负利率情形）
Vol	平值期权的正态波动率（bps单位）
In/Out Strikes	不同执行价的波动率报价（bps单位），执行价间隔按百分比列示

（2）实例解析（1Y期限）

执行价	-0.75%	-0.50%	...	10.00%
波动率	27.00	24.20	...	306.90

• 经济含义：
  对于1年期、执行价-0.75%的利率上限期权，市场报价波动率为27bps（即未来1年内，利率预期绝对波动的年化标准差为0.27%）

为什么是正态波动率？

利率市场的特性决定了采用Bachelier模型（正态波动率）：

1. 负利率可能性：表格中执行价出现负值（如-0.33%），对数正态模型无法处理
2. 线性敏感度：利率产品的DV01（利率变动1bp的价值变化）计算更匹配正态假设
3. 市场惯例：全球利率期权（如Cap/Floor、Swaption）普遍以bps报价波动率

五、波动率转换实务

外汇期权转换案例

给定：

• EUR/USD现价1.1000
• 1年期ATM隐含波动率12%（对数正态）
• 需转换为正态波动率

计算：

$$\sigma_n \approx 1.1000 \times 12\% = 0.132 \text{（即132pips）}$$

精确转换（T=1）：

$$\sigma_n = 1.1000 \times 12\% \times (1 + \frac{1}{2}0.12^2 \times 1) = 0.139 \text{（139pips）}$$

利率上限转换案例

给定：

• 3M LIBOR远期2.5%
• 正态波动率50bps
• 需转换为对数正态波动率

计算：

$$\sigma_{ln} \approx \frac{50bps}{2.5\%} = 20\%$$

精确转换：

$$\sigma_{ln} = \frac{50bps}{2.5\%} \left(1 - \frac{(50bps)^2 \times 1}{2 \times (2.5\%)^2}\right) \approx 18.5\%$$

六、Price Vol与Yield Vol的关联解析

Price Vol（价格波动率）和Yield Vol（收益率波动率）是金融市场中衡量资产价格或收益率波动的两种方式，它们的核心区别在于度量单位和适用场景，但可以通过数学关系相互转换。以下是两者的详细对比和关联：

1. 定义与核心区别

类型	Price Vol（价格波动率）	Yield Vol（收益率波动率）
定义	资产价格绝对变化的标准差（如美元、bps）	资产价格**百分比变化（收益率）**的标准差（如20%）
单位	与价格相同（如$5/年，50bps）	百分比（如20%）
适用模型	Bachelier（正态模型）	Black-Scholes（对数正态模型）
典型市场	利率衍生品（Cap/Floor）、商品期权	股票、外汇、债券收益率期权
允许负值？	是（如负利率）	否（对数变换保证正数）

2. 数学关系

(1) 短期近似关系

在短期或波动较小时，Price Vol（σₙ）和Yield Vol（σₗₙ）可以近似转换：

$$\sigma_n \approx S_0 \times \sigma_{ln}$$

例子：

• 股票现价$100，Yield Vol=20% →

$$\text{Price Vol} \approx 100 \times 0.20 = \$20/\text{年}$$

• 债券收益率现为2%，Yield Vol=10% →

$$\text{Price Vol} \approx 2\% \times 0.10 = 0.2\% \text{（即20bps）}$$

(2) 精确转换（考虑凸性调整）

长期或高波动时，需引入调整项：

$$\sigma_n = S_0 \sigma_{ln} \sqrt{T} \left(1 + \frac{1}{2} \sigma_{ln}^2 T \right)$$

$$\sigma_{ln} = \frac{\sigma_n}{S_0} \left(1 - \frac{\sigma_n^2 T}{2 S_0^2} \right)$$

例子：

• 若股票$100，Yield Vol=30%，T=1年 →

$$\sigma_n = 100 \times 0.30 \times \left(1 + \frac{0.3^2 \times 1}{2}\right) = 31.5 \text{美元/年}$$

3. 市场报价示例

(1) 利率市场（Price Vol主导）

• 产品：利率上限（Cap）
• 报价：50 bps（表示利率绝对波动的标准差为0.50%）
• 转换：若当前利率2%，等效Yield Vol ≈ 50bps / 2% = 25%

(2) 股票市场（Yield Vol主导）

• 产品：股票期权
• 报价：30%（表示股价年化收益率标准差30%）
• 转换：若股价$100，等效Price Vol ≈$30/年

七、市场惯例总结

市场类型	默认波动率类型	典型报价形式	主要产品案例
外汇	对数正态，Yield Vol	百分比波动率（12%）	EUR/USD期权
利率	正态，Price Vol	基点波动率（50bps）	LIBOR上限/下限
股票	对数正态，Yield Vol	百分比波动率（30%）	SPX期权
大宗商品	混合	两者并存	原油期权