利率互换的 Carry 与 Roll-down

在利率互换（Interest Rate Swap, IRS）交易中，持有期收益通常拆分为三部分：

1. Carry（持有成本／利差）
2. Roll-down（期限下滚收益）
3. 曲线移动影响

本文聚焦于前两者，并进一步讨论**远期起息互换（Forward-Starting Swap）**的 Roll-down 计算。

---

一、核心概念

1. Par-Swap Rate
   给定起息日 a 与到期日 b，使固定腿现值（PV）等于浮动腿现值时的固定付息利率：

   $$S(a \to b) = \frac{DF(a) - DF(b)}{\sum_i \tau_i\,DF(t_i)}$$

   其中 $DF(t)$ 为贴现因子，$\{t_i\}$ 为固定腿付息日，$\tau_i$ 为相邻付息日间年化天数。

2. Carry
   衡量「持有一笔现货互换」到某远期日（Horizon）所产生的年化净收益（不考虑曲线整体平移）。

   $$\text{Carry} = S(\mathrm{Horizon} \to \mathrm{Maturity}) - S(\mathrm{Start} \to \mathrm{Maturity})$$

   • 若以基点（bps）表示，再乘以 10 000。

3. Roll-down
   衡量「同一现货互换」因剩余期限缩短，在不考虑曲线整体平移情况下的年化收益：

   $$\text{Roll-down} = S(\mathrm{Start}\to\mathrm{Maturity}) - S(\mathrm{Start}\to(\mathrm{Maturity}-\mathrm{Horizon}))$$

   • 若以基点表示，再乘以 10 000。

4. 远期起息互换（Forward-Starting Swap）
   • Forward Tenor τ：互换从今天起延后 τ（如 1M、3M、6M、1Y）后才开始生效。
   • Underlying Tenor T：互换本身的固定腿名义期限（如 1Y、2Y、5Y）。
   • Forward Rate：

   $$F(\tau,T) = S(\text{Today}+\tau \;\to\;\text{Today}+\tau+T)$$

   • Forward Roll-down（下滚）
   选定一个Period Δ（如 1M 或 3M），表示“展开／收平”时要把起息延后期往前推 Δ：

   $$\text{Roll}_{fwd} = F(\tau,T) - F(\tau - Δ, T).$$

   同样×10 000 得 bps。

注意：远期起息互换在 Horizon 之前没有任何现金流，因此不存在 Carry，只能计算 Roll-down。

---

二、计算公式汇总

1. Spot-Swap (现货互换)：

   • Carry
     $\displaystyle C = S(\mathrm{H} \to \mathrm{M}) - S(\mathrm{0} \to \mathrm{M})$
   • Roll-down
     $\displaystyle R = S(\mathrm{0} \to \mathrm{M}) - S(\mathrm{0} \to \mathrm{M}-\mathrm{H})$

2. Forward-Swap (远期起息互换)：

   • Forward Rate
     $\displaystyle F(\tau,T) = S(\tau \to \tau+T)$
   • Forward Roll-down
     $\displaystyle R_{fwd} = F(\tau,T) - F(\tau - Δ,\,T)$

以上所有利率差，若需以基点（bps）表示，乘以 10 000。

---

三、业务计算步骤

1. 准备贴现曲线
   获取 OIS 或 Libor 曲线，能够输出任意日期 $t$ 的贴现因子 $DF(t)$。

2. 确定关键日期与参数

   • Spot-Swap：
     • Start = 今日
     • Horizon = Start + H
     • Maturity = Start + M
   • Forward-Swap：
     • Forward Tenor τ
     • Underlying Tenor T
     • Period Δ（用于 Roll-down）

3. 计算平价互换利率

   • Spot
     • $S_0=S(0\to M)$
     • $S_H=S(H\to M)$
     • $S_r=S(0\to M-H)$
   • Forward
     • $F_τ=F(\tau,T)=S(\tau\to\tau+T)$
     • $F_{τ-Δ}=F(\tau-Δ,T)$

4. 求差并转换基点

   • Spot-Carry = $(S_H - S_0)\times10\,000$
   • Spot-Roll-down = $(S_0 - S_r)\times10\,000$
   • Forward-Roll-down = $(F_τ - F_{τ-Δ})\times10\,000$

---

四、数值示例

1. Spot-Swap (5Y，总持有 1Y)

   • $S(0\to5)=3.00\%$
   • $S(1\to5)=3.75\%$
   • $S(0\to4)=2.50\%$
     Carry = (3.75−3.00)×10 000 = 75 bps/年
     Roll-down = (3.00−2.50)×10 000 = 50 bps/年

2. Forward-Swap

   • Underlying = 1Y，Forward Tenor = 3M，Period Δ=1M
   • $F(3M,1Y)=S(3M\to15M)=1.516\%$
   • $F(2M,1Y)=S(2M\to14M)=1.532\%$
     Forward Roll-down = (1.516−1.532)×10 000 = −1.6 bps

---

五、参考：Bloomberg Forward-Swap 矩阵

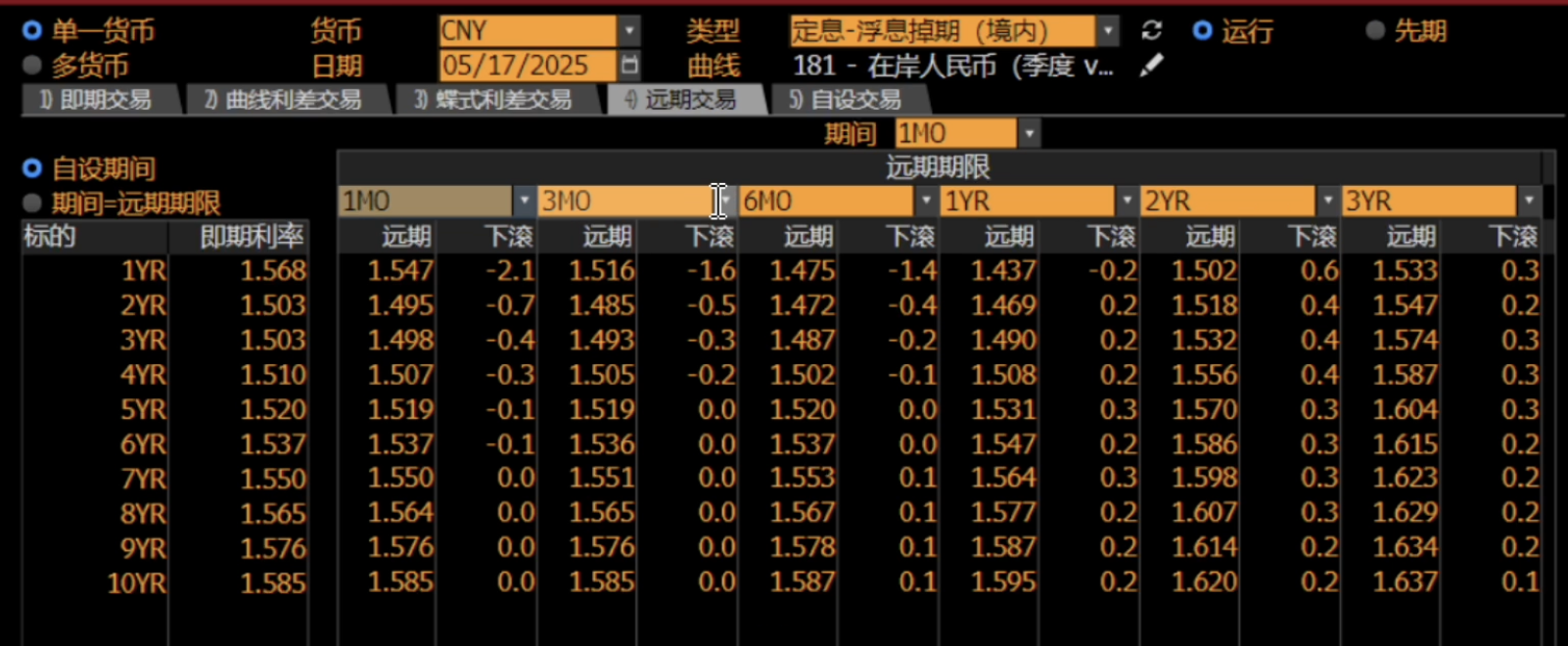
横向

• Period（界面右上角）：滚动步长 Δ（如 1MO、3MO）
• Forward Tenor（列头）：互换起息延后期 τ（如 1MO、3MO、6MO、1YR…）

纵向

• Underlying（行头）：互换名义期限 T（如 1YR、2YR、3YR…）

单元格显示

• 远期 = $F(\tau,T)$
• 下滚 = $[F(\tau,T) - F(\tau-Δ,T)]×10\,000$ bps