正态分布相关的概念

上海子午线大约 7 分钟

正态分布相关的概念

访问猛犸期权定价系统，支持外汇期权和结构化产品定价估值！

在统计学中，正态分布是一个核心概念，它与标准正态分布、标准偏差、累计分布函数（CDF）、百分位数和分位数密切相关。以下是对这些概念的详细解释，包括它们的定义、数学公式及应用场景。

1. 正态分布

定义

正态分布（Normal Distribution）是一种重要的连续概率分布，形状为对称的钟形曲线，广泛用于描述自然界中大量随机变量的分布（如身高、体重、考试成绩等）。

概率密度函数（PDF）公式

正态分布的概率密度函数为：

f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}

$\mu$ ：均值，决定分布的中心位置。
$\sigma$ ：标准偏差，衡量数据的离散程度，决定曲线的宽度。
$x$ ：随机变量的值。

特点

对称性：关于均值 $\mu$ 左右对称。
峰值位置：概率密度函数的最大值出现在均值 $\mu$ 。
尾部特性：分布的尾部逐渐趋近于零（无限接近但不为零）。
68-95-99.7 规则：
- 68% 的数据位于 $[\mu - \sigma, \mu + \sigma]$ 。
- 95% 的数据位于 $[\mu - 2\sigma, \mu + 2\sigma]$ 。
- 99.7% 的数据位于 $[\mu - 3\sigma, \mu + 3\sigma]$ 。

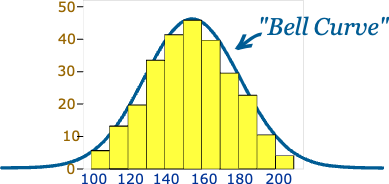
正态分布的直方图解释

直方图是将数据分为若干区间后绘制的柱状图，用于可视化数据的分布。
如果一组数据服从正态分布，其直方图会呈现出对称的钟形，数据集中在均值附近，两侧逐渐减少。

示例：以一组均值为 $150$ ，标准偏差为 $30$ 的数据为例，其直方图可能如下：

2. 标准正态分布

定义

**标准正态分布（Standard Normal Distribution）**是正态分布的一种特殊形式，具有以下参数：

均值 $\mu = 0$
标准偏差 $\sigma = 1$

概率密度函数（PDF）公式

标准正态分布的概率密度函数为：

f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}

特点

因为均值为 0，分布的中心在 0。
标准正态分布是所有正态分布的基准，可以通过标准化公式将任意正态分布转化为标准正态分布。

标准化公式

将任意正态分布转化为标准正态分布：

z = \frac{x - \mu}{\sigma}

- $z$ ：标准化后的值（也称为 Z 分数）。
- $x$ ：原始数据值。
- $\mu$ ：均值。
- $\sigma$ ：标准偏差。

3. 标准偏差（Standard Deviation, $\sigma$ ）

定义

标准偏差是衡量数据分布离散程度的指标，表示数据点偏离均值的平均程度。

公式

标准偏差是方差的平方根：

\sigma = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n}}

- $\bar{x}$ ：数据的均值。
- $x_i$ ：第 $i$ 个数据点。

在正态分布中的意义

标准偏差决定了正态分布的曲线宽度。
标准偏差小：数据集中，曲线较窄。
标准偏差大：数据分散，曲线较宽。

4. 正态分布与标准差的关系

正态分布的中心是均值 ( $\mu$ )，其扩展范围由标准差 ( $\sigma$ ) 决定。图中展示了正态分布的三个区间，分别涵盖了不同的概率范围：

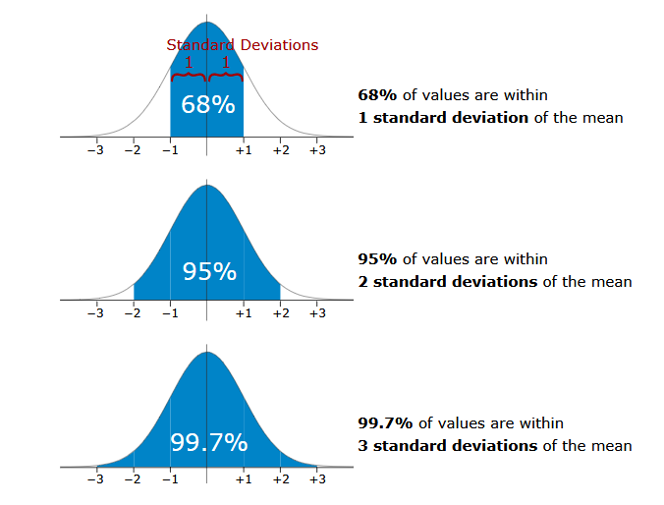
68% 的数据在 ±1 个标准差范围内

范围： $[ \mu - \sigma, \mu + \sigma ]$
这意味着：
- 数据中有 68% 的值会落在均值左右 1 个标准差的范围内。
- 例如，如果均值为 $\mu = 150$ ，标准差为 $\sigma = 30$ ，则 68% 的数据会落在 $[120, 180]$ 范围内。

95% 的数据在 ±2 个标准差范围内

范围： $[ \mu - 2\sigma, \mu + 2\sigma ]$
这意味着：
- 数据中有 95% 的值会落在均值左右 2 个标准差的范围内。
- 例如，如果均值为 $\mu = 150$ ，标准差为 $\sigma = 30$ ，则 95% 的数据会落在 $[90, 210]$ 范围内。

99.7% 的数据在 ±3 个标准差范围内

范围： $[ \mu - 3\sigma, \mu + 3\sigma ]$
这意味着：
- 数据中有 99.7% 的值会落在均值左右 3 个标准差的范围内。
- 例如，如果均值为 $\mu = 150$ ，标准差为 $\sigma = 30$ ，则 99.7% 的数据会落在 $[60, 240]$ 范围内。

2. 图中每部分的意义

中间的 68% 部分（±1σ）：
- 表示多数数据集中在均值附近。
- 68% 的概率意味着大部分数据点会与均值接近。
扩展到 ±2σ 的区域（95%）：
- 包括了更广范围的数据。
- 这表明极端值（离均值较远的值）在正态分布中较少。
扩展到 ±3σ 的区域（99.7%）：
- 包含了几乎所有数据点（99.7%）。
- 剩下的 0.3% 数据点是极端的异常值。

5. 累计正态分布（CDF, Cumulative Distribution Function）

定义

**累计分布函数（CDF）**描述随机变量 $X$ 小于或等于某个值 $x$ 的累积概率：

F(x) = P(X \leq x)

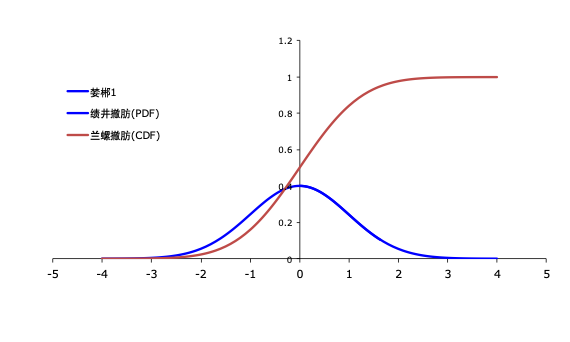
在正态分布中的意义

CDF 是正态分布概率密度函数（PDF）的积分。
CDF 表示正态分布曲线左侧区域的概率。
在标准正态分布中，CDF 通常用符号 $\Phi(x)$ 表示。

示例

- $\Phi(0) = 0.5$ ：均值处的累计概率为 50%。
- $\Phi(-1) \approx 0.1587$ ：标准正态分布中，值小于 $-1$ 的概率约为 15.87%。

6. 百分位数（Percentile）

定义

百分位数（Percentile）是将数据分布按百分比划分的指标，表示某个值在数据分布中所处的相对位置。

公式

第 $p\%$ 百分位数指数据中有 $p\%$ 的值小于或等于该值。

示例：

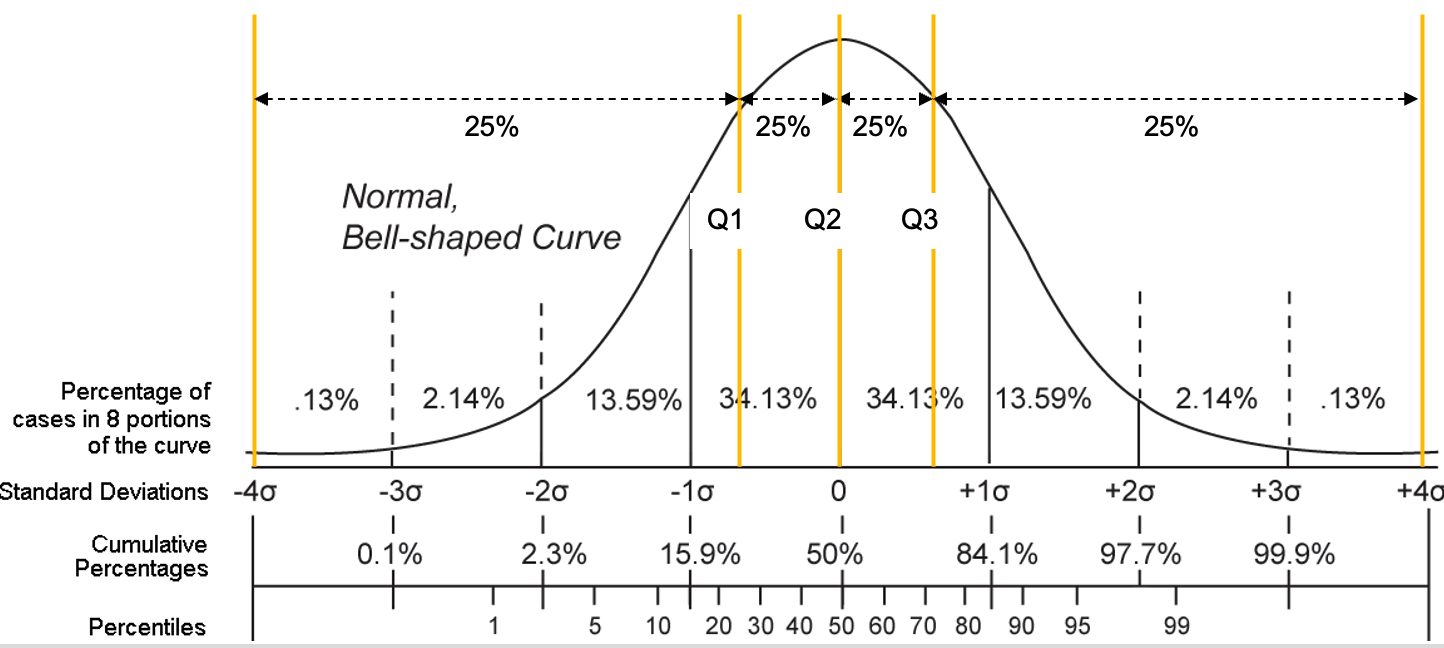
第 25 百分位数（P25）：数据中有 25% 的值小于或等于该值，称为第一四分位数（Q1）。
第 50 百分位数（P50）：数据中有 50% 的值小于或等于该值，等同于中位数。
第 75 百分位数（P75）：数据中有 75% 的值小于或等于该值，称为第三四分位数（Q3）。

7. 分位数（Quantile）

定义

分位数（Quantile）是将数据分布按比例划分的位置值，是百分位数的推广。

公式

分位数按照比例 $q$ 划分数据。例如：
- $q = 0.25$ ：第 0.25 分位数（或第 25 百分位数）。
- $q = 0.5$ ：第 0.5 分位数（或中位数）。

分位数与百分位数关系

百分位数是分位数的百分比表示：

Percentile = Quantile \times 100

示例：

0.25 分位数 = 第 25 百分位数。
0.75 分位数 = 第 75 百分位数。

8. 总结对比

概念	定义	公式/特点
正态分布	一种连续概率分布，呈对称的钟形曲线，均值 $\mu$ 和标准偏差 $\sigma$ 决定其形状和位置。	$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}$
标准正态分布	特殊的正态分布，均值 $\mu = 0$ ，标准偏差 $\sigma = 1$ 。	$f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$
标准偏差	衡量数据离散程度的指标，表示数据偏离均值的程度。	$\sigma = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n}}$
累计分布函数（CDF）	表示随机变量 $X$ 小于或等于某值 $x$ 的累积概率。	$F(x) = P(X \leq x)$
百分位数（Percentile）	按百分比划分数据分布的位置，例如第 25 百分位数表示 25% 的数据小于或等于该值。	$Percentile = Quantile \times 100$
分位数（Quantile）	按比例（如 0.25, 0.5, 0.75）划分数据分布的位置值，是百分位数的推广。	$q = \frac{\text{位置值}}{\text{总数}}$

8. 应用场景

正态分布：用于描述自然现象数据（如身高、体重）。
标准正态分布：用于概率计算和假设检验。
标准偏差：衡量数据波动性（如股票收益波动）。
累计分布函数（CDF）：计算概率和绘制分布曲线。
百分位数和分位数：用于描述数据分布，特别是在偏态分布中（如收入分布、考试成绩）。