In-Depth Analysis: Construction of EURUSD Option Volatility Surface, Pricing, and Greek Calculations in Murex System – A Comparative Study with MCPx and Bloomberg

Abstract

This article takes the EURUSD currency pair as an example, aiming to detail the replication of the foreign exchange option volatility surface construction process, option pricing model, and Greek calculation methods within the globally leading risk and trading system, Murex. We will first construct a complete volatility surface based on public market data (presented as images), followed by option pricing. The core of the article will conduct a comparative analysis of the differences in pricing results and Greeks (especially the queried Delta values) between Murex and another mainstream system, MCPx, using Bloomberg Terminal calculations as a third-party benchmark for horizontal validation. The goal is to explore the sources of differences and assess the accuracy of the calculations.

Part 1: Introduction and Background

Research Motivation:
- FX options are among the most active derivatives in financial markets, and their accurate pricing and risk management are crucial for institutions.
- As an industry benchmark, Murex's internal models and calculation logic are the core of risk control for many financial institutions. However, calculated results in practice (such as Delta) sometimes deviate from traders' intuition or other systems, warranting in-depth investigation.
- Systematic comparison (Murex vs. MCPx vs. Bloomberg) can validate the impact of model assumptions, parameter settings, and numerical methods, providing reference for practical operations.
Objectives and Scope:
- Objective: To replicate Murex's volatility surface, pricing, and analyze Greeks.
- Scope: Focus on EURUSD spot rate, plain vanilla European options.
- Comparative Systems: Murex MX.3, MCPx (Mathema Calculation Plus), Bloomberg OVML.
Tools and Data Used:
- Assumption: We possess screenshots from the Murex system (volatility matrix, pricing results).
- Primary replication tool: MCPx Excel.
- Market data date: 【2024-03-25】.

Part 2: Replication of Murex Volatility Surface Construction

Market Data Input (Display Images):
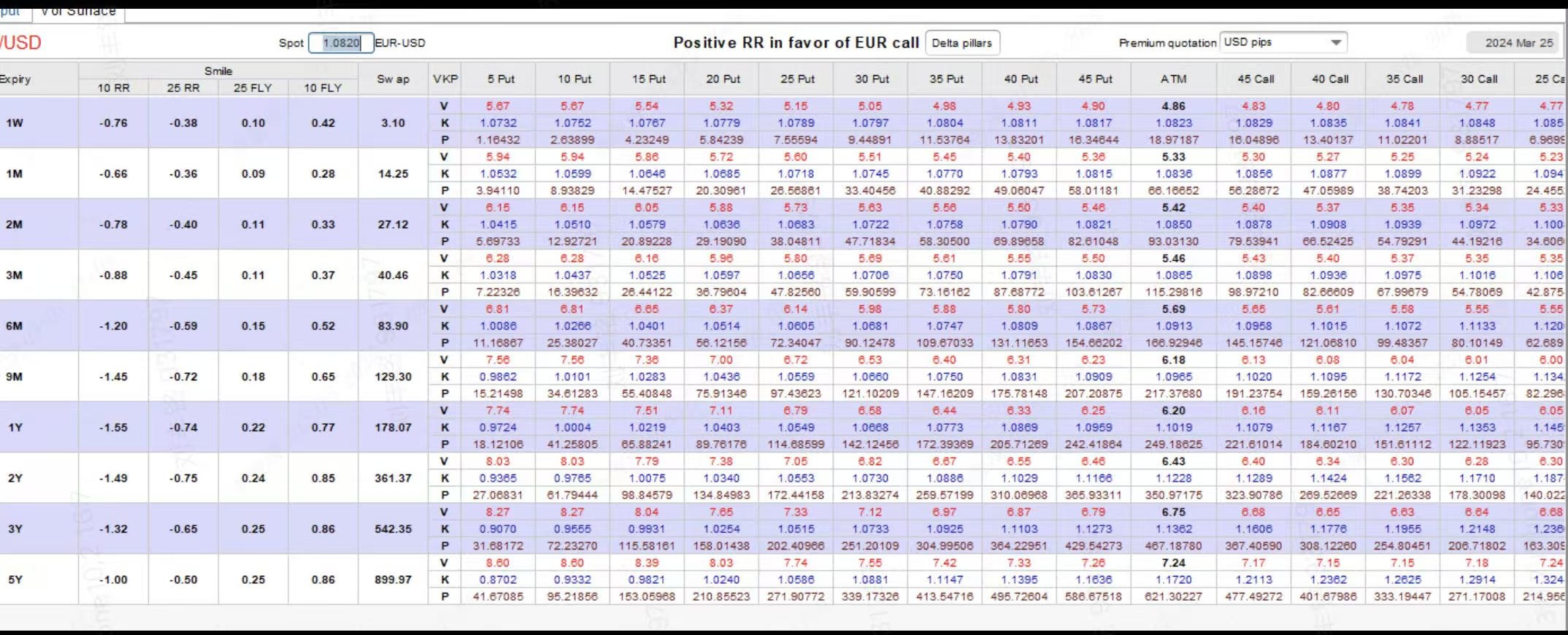
- Image (Left): Murex 10RR, 25RR, ATM, 25BFLY, 10BFLY volatility matrix screenshot. Shows market volatility quotes for different tenors (1W, 1M, 3M, 6M, 1Y).
- Image (Right): Shows the result of Murex processing the volatility, including the corresponding implied strike prices and volatilities for 19 Delta points from 5D Put, 15D Put, ..., to 15D Call, 5D Call.
eb32511f746a085022de58da4a839393
- The relationships between RR, BFLY (BF), and Call Delta, Put Delta here are:
  - RR = σ(25Δ Call) - σ(25Δ Put)
  - BF = (σ(25Δ Call) + σ(25Δ Put))/2 - σ(ATM)
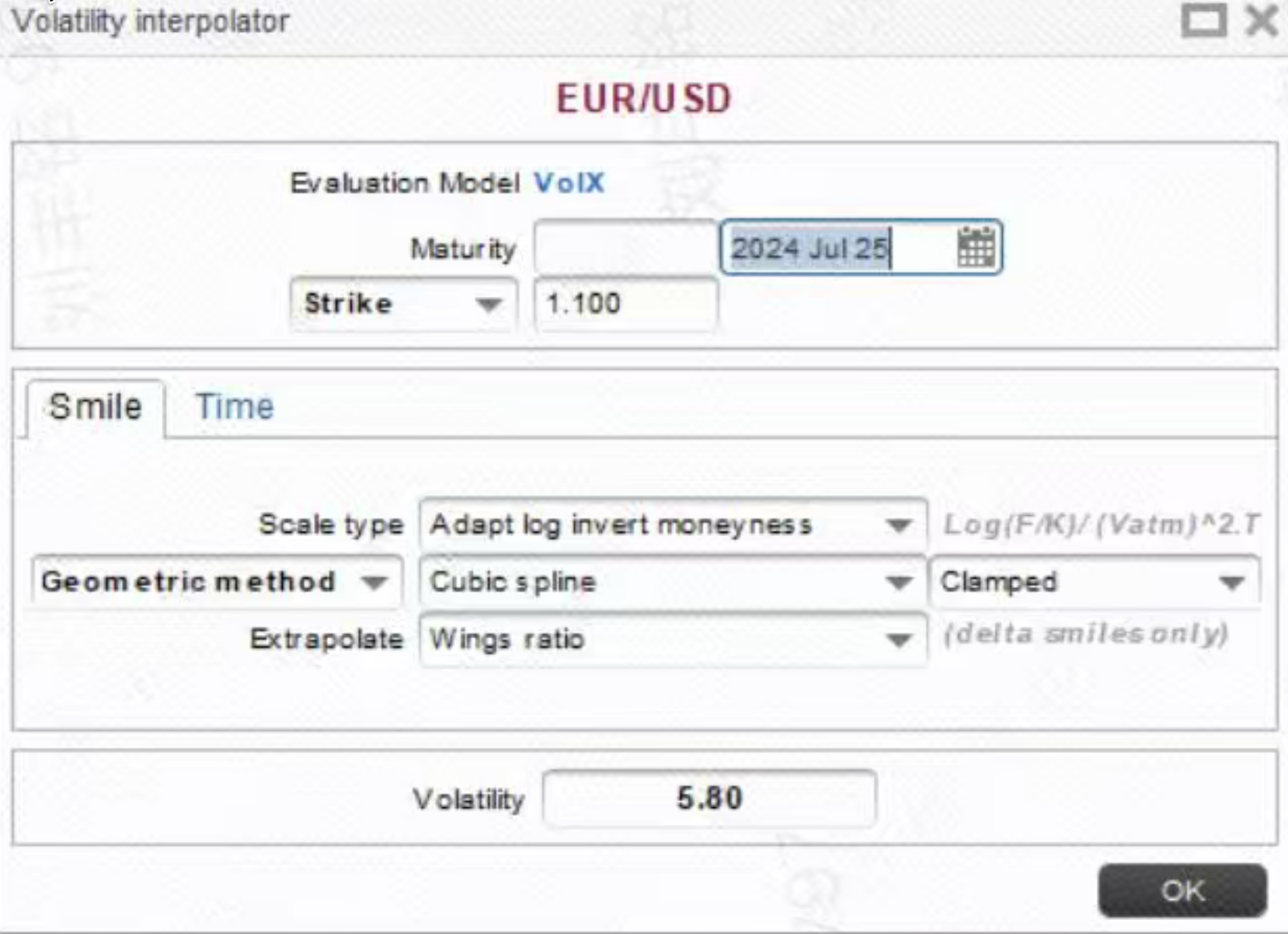
- Murex construction parameters, as shown below:
  - Interpolation Method: Cubic Spline (Clamped)
  - Tail Adjustment: Wing Ratio (Not set)
Construction Method Overview:
The following are simplified steps. For the detailed construction process, refer to: FX Option Volatility Surface Construction
- Step 1: Interpolate to build the baseline curve. Perform interpolation (cubic spline) along the tenor dimension separately for the three data sets: ATM, RR, BF, to obtain σ_ATM(τ), RR(τ), BF(τ) for any tenor.
- Step 2: Construct the smile curve analytically. For each given tenor τ, use the interpolated RR(τ) and BF(τ) to solve for the volatilities of the 25Δ call and put options:
  - σ_25C = σ_ATM + BF + RR/2
  - σ_25P = σ_ATM + BF - RR/2
- Step 3: Fit the entire smile curve. Murex typically uses Cubic Spline by default to extrapolate the implied volatility across the entire Delta space from the three benchmark points (25Δ Put, ATM, 25Δ Call). This article will use the Cubic Spline method for replication, as it is more common in the FX market.
- Step 4: Two-dimensional interpolation. Finally, we obtain a two-dimensional volatility surface function σ(Δ, τ).
Replication Result Comparison (Display Image):
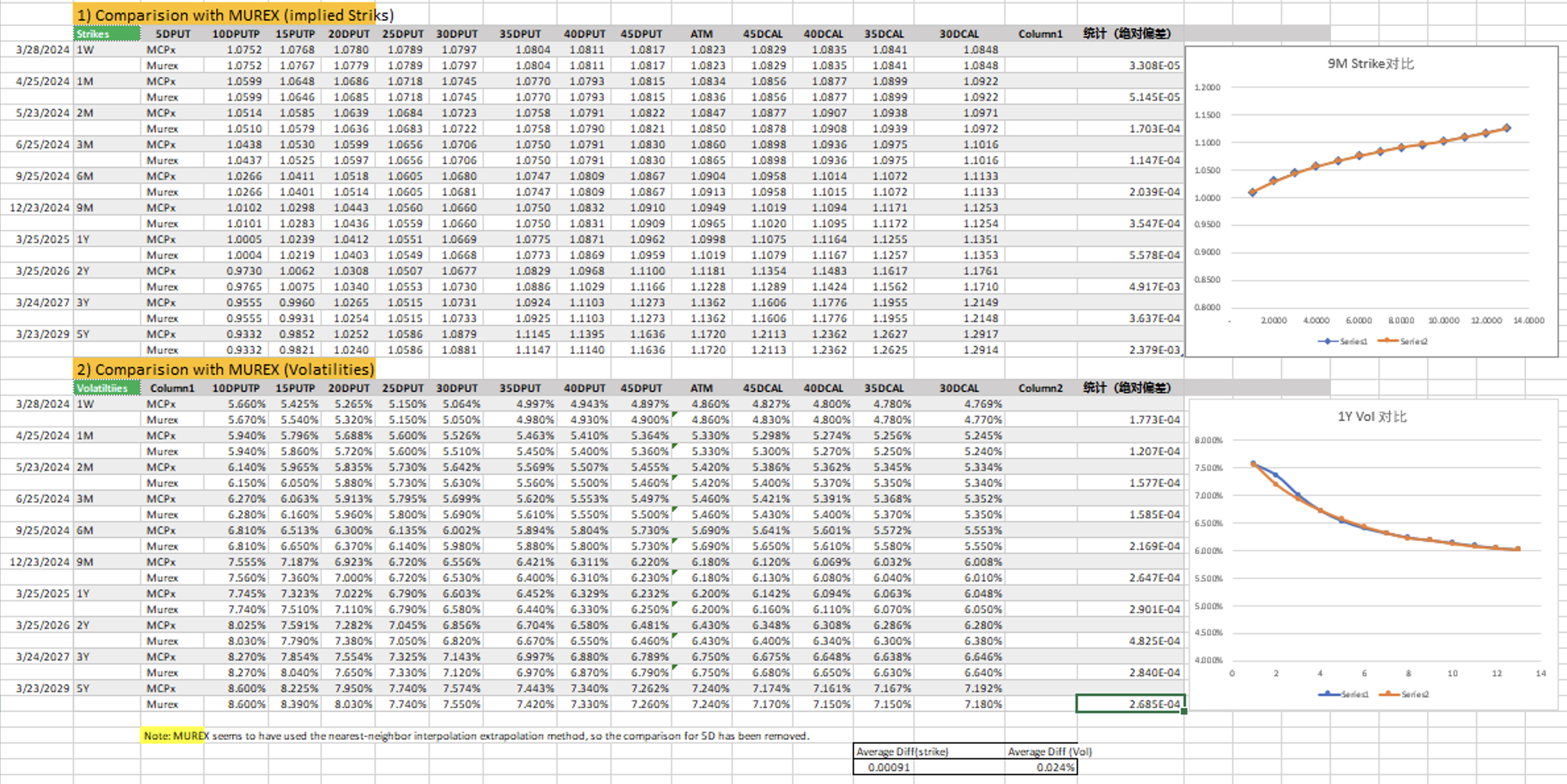
- Table 1: Comparison between replication results and Murex screenshot. Average strike deviation: 0.00091, average volatility deviation: 0.024%, basically consistent!
As the Bloomberg volatility surface cannot be modified, comparison with it is omitted here.

Part 3: Option Pricing and Greek Calculation

Pricing Model:
- The standard pricing model for FX options is the Garman-Kohlhagen model (an extension of the Black-Scholes model considering two currency interest rates).
- Pricing Formulas:
  C = S_0 * e^(-r_quote * T) * N(d1) - K * e^(-r_base * T) * N(d2)
  P = K * e^(-r_base * T) * N(-d2) - S_0 * e^(-r_quote * T) * N(-d1)
  where d1 = (ln(S_0/K) + (r_base - r_quote + σ²/2)*T) / (σ√T), d2 = d1 - σ√T
  - S_0: EURUSD spot rate (e.g., 1.0850)
  - r_base: Base currency interest rate (EUR, e.g., Euribor)
  - r_quote: Quote currency interest rate (USD, e.g., Libor)
  - K: Strike price
  - T: Time to expiration
  - σ: Volatility interpolated from the constructed volatility surface based on the option's Delta and tenor.
    For details, refer to: Black-Scholes Model
Greek Calculation:
- Delta (Δ): The first derivative of the option price with respect to the spot rate. This is the key focus of this article.
  - G-K model theoretical Delta: Δ_call = e^(-r_quote * T) * N(d1)
  - Point of Inquiry: Murex's Delta calculation might not directly use this formula. In the FX market, Delta often has different conventions:
    - Spot Delta: As above.
    - Forward Delta: Δ_forward = e^(-r_base * T) * N(d1) (more commonly used for quoting among FX option traders).
    - Premium Adjusted Delta: For investors whose base currency is not USD, an adjustment term is introduced to account for the fact that the option premium itself is in a foreign currency.
- Other Greeks (Gamma, Vega, Theta, Rho) will also be calculated using standard formulas.
  For details, refer to: Greeks

Part 4: Horizontal Comparison and Accuracy Discussion: Murex vs. MCPx vs. Bloomberg

System Introduction:
- Murex MX.3: An integrated front, middle, and back-office system using internal models and parameters.
- MCPx: An independent third-party pricing service providing market consensus-based valuations, intended as a verification tool for middle/back-office.
- Bloomberg OVML: A widely used industry pricing tool, serving as a reliable benchmark.
- Refinitiv WS: A widely used industry pricing tool.
Comparison Methodology:
- Obtain calculation results from all four systems for the same option (identical date, spot rate, interest rates, strike price, tenor).
- Focus on differences in Greek values.

Results Presentation and Analysis:

Table 2: Comparison of Key Outputs from MCPx, Bloomberg, Refinitiv WS, and Murex Systems

Greek Metric	MCP	Bloomberg	Refinitiv WS	MUREX	Difference Description
Delta%(EUR)	35.2972%	35.2973%	-	37.3200%	MCPx matches BBG exactly, Murex has minor difference
ForwardDelta%(EUR)	35.7756%	35.7757%	36.5560%	37.8000%	MCPx matches BBG exactly, Murex has minor difference
Gamma(EUR)	117250.52	117250.59	121060.00	13.35	MCPx matches BBG exactly, Murex has minor difference
Vega(EUR)	2134.14	2145.10	2145.00	-	MCPx slightly differs from BBG/WS, BBG/WS consistent
Theta(EUR)	-61.89	-47.09	-6000.00	-	MCPx differs from BBG, and also differs from WS
Vanna(EUR)	23514.078	22671.000	2.544%	-	Differences exist across all four systems
Volga(EUR)	5055.253	50.550	0.505%	-	MCPx is basically consistent with BBG
Rho(EUR)	1179.794	1199.140	0.118%	-	MCPx differs from BBG, and also differs from WS
Phi(EUR)	-1225.24	-1225.24	-	-	MCPx is basically consistent with BBG
Price(USD)	83.129	83.129	83.14	83.315	MCPx matches BBG exactly, Murex shows slightly larger difference
Delta%(USD)	36.0655%	36.0656%	-	-36.7100%	MCPx matches BBG exactly, Murex has minor difference
ForwardDelta%(USD)	36.5543%	36.5544%	-	-37.3800%	MCPx matches BBG exactly, Murex has minor difference
Gamma(USD)	126865.07	N/A	-	13.13	-
Vega(USD)	2320.99	2321.00	-	23.50	MCPx is basically consistent with BBG, Murex has minor difference
Theta(USD)	-66.96	-50.95	-	-0.76	MCPx differs from BBG, and also differs from WS, Murex
Vanna(USD)	25442.232	27528.460	-	2.676	Differences exist across all four systems
Volga(USD)	5469.784	54.700	-	0.544	MCPx is basically consistent with BBG, Murex has minor difference
Rho(USD)	1276.537	1297.470	-	13.466	MCPx differs from BBG, and also differs from WS, Murex
Phi(USD)	-1325.71	-1325.71	-	-13.75	MCPx is basically consistent with BBG, Murex has minor difference

Summary:

MCPx results are completely consistent with Bloomberg, verification passed.
Some indicators from the Murex system show slight differences compared to MCPx and Bloomberg.
Differences are explainable: The differences with MUREX (factor of 100) and Refinitiv WS (factor of 100) are both caused by "differences in unit definitions", not model errors.
Conclusion: The MCPx system is accurate and reliable. Differences with other systems can be eliminated simply by unifying units. Reference: [3. How to Distinguish Greek Value Units?]

Part 5: Conclusion

Successfully replicated the construction of the Murex volatility surface and the calibration process. The differences in the calibrated Strike and Volatility results are relatively small (average Strike difference 0.00091, average Volatility difference 0.024%).
Successfully replicated the Murex volatility surface construction and option pricing process. The core price, Delta, Gamma, Vega and other Greeks are highly consistent with other systems.
Compared with the Bloomberg system and the Refinitiv WS system, it was found that MCPx results are completely consistent with Bloomberg. Some indicators from the Murex system show slight differences compared to MCPx and the Bloomberg system.