债券骑乘策略(Riding the Yield Curve)
大约 4 分钟
债券骑乘策略(Riding the Yield Curve)
一、什么是骑乘策略?
骑乘策略是一种利用收益率曲线的正斜率特征,通过持有中长期债券至剩余期限缩短,获取资本利得的主动投资策略。其核心逻辑是:
- 长期债券收益率通常高于短期债券(正斜率曲线)。
- 随着时间推移,债券剩余期限缩短,其收益率沿曲线下滑,价格自然上涨。
- 投资者通过"骑乘"收益率曲线,在持有期内获得利息收入 + 资本利得的超额收益。
二、骑乘策略的收益来源分解
根据市场标准术语,骑乘策略的总收益可拆解为以下五大组成部分:
1. 票息收入(Coupon Income)
- 定义:持有期内债券定期支付给你的票面利息之和。
- 量化:
其中 是第 次付息额, 为持有区间。
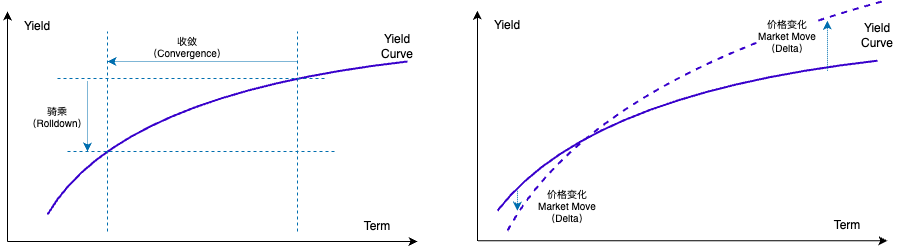
2. 收敛收益(Convergence)
- 定义:假设债券的到期收益率(YTM)不变,仅因剩余期限从 变为 而引起的价格向面值(或基准价格)收敛的部分。
- 量化:
其中两项都是在同一个到期收益率 下,对应不同剩余期限的定价。
3. 骑乘收益(Rolldown Return)
- 定义:在收益率曲线形状和水平不变的假设下,债券剩余期限沿曲线"往下滚"——也就是由 → 时,所对应的到期收益率从 → 带来的额外价格提升。
- 量化(仅曲线斜率部分):
- 合理解释:Rolldown = Convergence + 这个斜率效应。
- 示例:买入5年期债券(YTM=4%),1年后剩余4年,若4年期收益率降至3.5%,价格上升的价差即为骑乘收益。
4. 再投资收益(Reinvestment Return)
- 定义:持有期内拿到的每笔票息,在当时的市场利率下再投资、并滚动到持有期结束时得到的收益。
- 量化:如果第 次票息在 收到并以再投资率 滚动到 ,
5. 市场变化收益(Market Move Impact)
- 定义:持有期结束时,真实收益率曲线从 变为 (平移、陡度改变等)所带来的价格差。
- 量化:
- 风险属性:不可控的市场风险,可能抵消或增强骑乘收益。
6.总收益公式:
三、Carry 与 Roll-down
在实际交易中,Carry 与 Roll-down 是两个最常被用来拆分持有期收益的概念:
Carry(持有收益)
- 定义:持有债券期间获得的净票息收入,扣除融资(回购)成本后,可再投资产生的收益也归入此项。
- 对应分解:
- 票息收入
- 再投资收益
- (若需)减去融资成本
Roll-down(骑乘收益)
- 定义:假设收益率曲线水平不变,仅因剩余期限从 (T) → (T-\Delta t) 带来的价格变化;此项包含 收敛 与 斜率滚动 两部分:
- 收敛(Pull-to-Par):同一 YTM 下,债券走向到期、价格向面值收敛;
- Rolldown Return:同一曲线下,不同剩余期限对应不同 YTM,期限缩短带来的那部分价差。
- 定义:假设收益率曲线水平不变,仅因剩余期限从 (T) → (T-\Delta t) 带来的价格变化;此项包含 收敛 与 斜率滚动 两部分:
Carry + Roll-down = 总资本利得
不计市场行情变动的情况下,一年持有期的预期回报近似等于当年对应的第二年远期利率:
要点:
- 将 Carry 定义为“票息 + 再投资 – 融资”,Roll-down 定义为“收敛 + 期限滚动”,有助于在不同市场环境下精确度量持有期收益。
- 在倒挂曲线下,长端多头的 Carry 常为负;而 Roll-down 也可能因短端高于长端而受限。
四、骑乘收益(Rolldown Return)的详细计算
核心假设
- 收益率曲线形态和水平不变(仅债券期限缩短,YTM沿曲线下滑)。
计算步骤
- 初始价格(买入时)
根据债券的剩余期限和当前收益率曲线,计算全价(含应计利息)。
公式:可以理解为通过收益率来计算全价,如果已知收益率
- 未来价格(持有后)
根据缩短后的剩余期限,从曲线上获取新的YTM,重新计算全价。
示例:- 初始:5年期债券,YTM=4%,价格=95.62元。
- 1年后:剩余4年,YTM沿曲线下滑至3.5%,价格=97.16元。
- 骑乘收益 = 97.16 - 95.62 = 1.54元。
关键影响因素
- 收益率曲线的斜率:曲线越陡峭,骑乘收益越高。
- 债券的凸性(Convexity):高凸性债券对收益率下滑更敏感。