跳至主要內容

Greeks

上海子午线大约 15 分钟

Greeks

访问猛犸期权定价系统，支持外汇期权和结构化产品定价估值！
访问猛犸期权定价系统，支持外汇期权和结构化产品定价估值！

Grees值基本概念

‘希腊字母’是代表期权权利金敏感度的数量。它们用于预测一份期权合约的风险。

  • Delta -及标的货币对价格变化的期权权利金的变化​
  • Gamma - 衡量当标的货币对价格变化时Delta (Δ) 率的变化​
  • Vega - 衡量标的货币对的期权权利金如何受波动率(σ) 变化的影响​
  • Theta -衡量期权权利金对时间流逝(τ)，或者“时间衰竭”的敏感度​
  • Rho -衡量期权权利金对利率(r)变化的敏感度

Delta

Delta[Δ=∂P∂S][\Delta=\frac{\partial\mathrm{P}}{\partial\mathrm{S}}]，是标的物价格变化的期权权利金的变化​
汇率变动1个单位，期权价值变动多少​
示例：50看涨期权，90天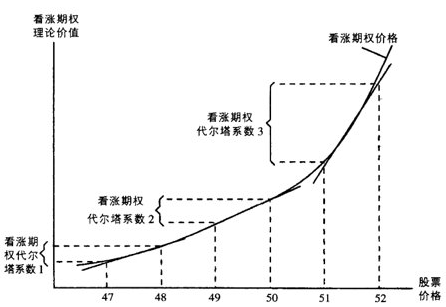
Delta

从行权的可能性的角度表述，Delta是指普通期权到期执行的可能性（反映期权到期时成为价内的概率）​

  • 以买入看涨期权为例，随着到期日的临近，​ITM的Delta将趋近于1，OTM的Delta将趋近于0
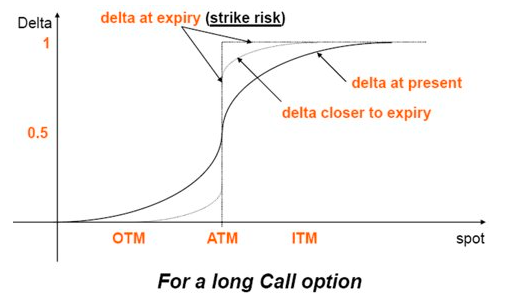
    DeltaChange

  • 以卖出看涨期权为例，随着到期日的临近，​ITM的Delta将趋近于-1，OTM的Delta将趋近于0
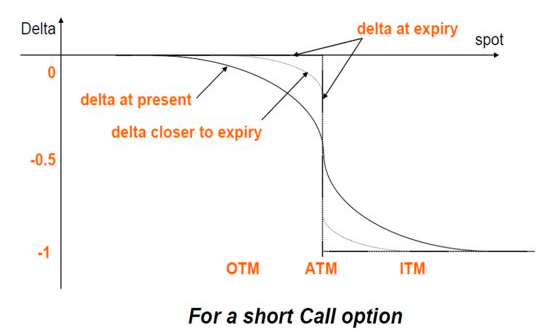
    DeltaChange

Gamma系数 – Delta系数的变动率

Gamma [Γ=∂Δ∂S=∂2P∂S2] [\Gamma=\frac{\partial\Delta}{\partial\mathrm{S}}=\frac{\partial^2\mathrm{P}}{\partial\mathrm{S}^2}] ：
衡量当标的货币对价格变化时Delta (Δ) 率的变化。这里的问题是： 在现货价格发生变化后，Delta的变化幅度会有多大？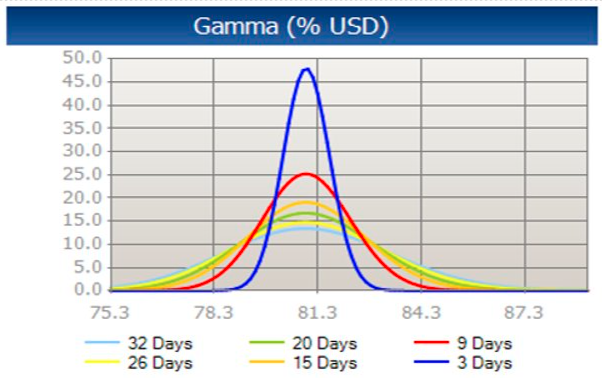
Gamma

Gamma值有正负。正的Gamma值意味着期权的Delta值会随标的物的价格上升而增加，随标的物价格下降而下降；负的Gamma意味着Delta值会随标的物的价格上升而减小，随标的物的价格下降而上升​

一般来说，所有买入期权拥有正Gamma 值，所有卖出期权拥有负Gamma值​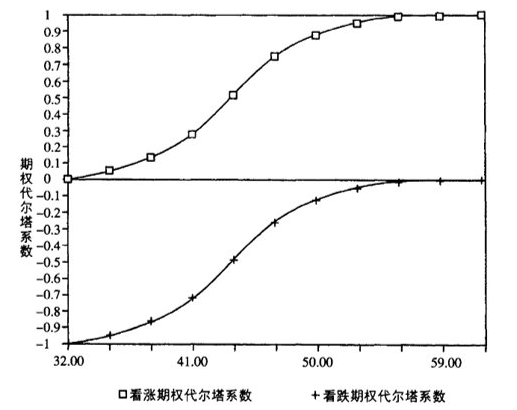
Gamma
​

Theta系数 – 因时减值（Time Decay）

Theta [Θ=−∂P∂τ]{[\Theta=-\frac{\partial\mathrm{P}}{\partial\tau}]}
：衡量期权权利金对时间流逝(τ)，或者“时间衰竭”的敏感度。随着期权合约接近截止期，时间衰竭也加速。

  • Theta对于买入看涨期权和买入看跌期权为负值，对于卖出 看涨期权和卖出看跌期权为正值​
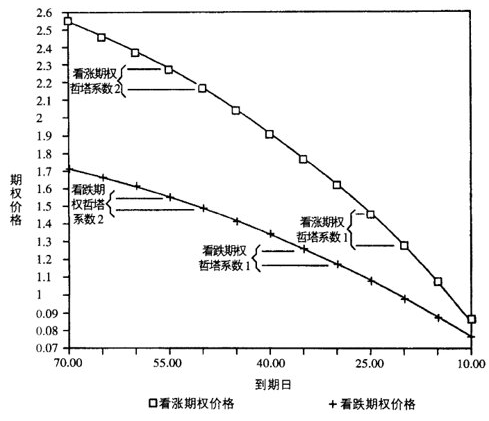
  • 相同期限的期权，ATM的Theta绝对值大；越接近到期日，Theta 绝对值越大​
  • 当期权期限很长时，Theta 很小，快到期时迅速增加
    Theta

Vega – 波动率的变化

Vega [v=∂P∂σ][v=\frac{\partial\mathrm{P}}{\partial\sigma}]：衡量标的物的期权权利金如何受波动率(σ) 变化的影响。它表示为当波动 率上升或下降1%时，期权所获得或失去的金钱数量。Vega在波动较大的市场尤其重要，可以监控一份期权权利金。​

  • Buy Vanilla option (call/put) → Vega为正值​
  • Sell Vanilla option (call/put) → Vega为负​

Rho – 利率变化敏感度​

Rho [P=∂P∂r]\mathrm{[P=\frac{\partial P}{\partial r}]}：衡量期权权利金对利率(r)变化的敏感度。​

  • 对于看涨期权，rho是正值，看跌期权的rho为负值。换言之，利率上升，看涨期权的价格会上涨，而看跌期权的价格会下跌。​
  • 我们将买入看涨期权作为买入股票的替代交易，买入股票是要占用资金，但是买入看涨期权是不占用资金的。这样节省的资金可以产生利息收入，所以利率水平高时，看涨期权的价格会升高。​
  • 利率被认为是期权定价模型所有参数中最不重要的一个。​

Rho 和 Phi：

Rho 衡量的是投资组合价值对利率水平变化的敏感性。一般来说，货币期权有两种 Rho：一种是针对国内利率，另一种是针对外币利率。它测量的是资产组合价值对利率变化的敏感性。对于看涨期权，Rho 的值通常是正的，而对于看跌期权，Rho 的值通常是负的。

Rho 表示由于国内货币利率的微小变化，期权溢价的预期变化。Phi 表示由于外币利率的微小变化，期权溢价的预期变化。
参考：
The Complete Guide to Option Pricing Formulas-Haug.pdf, P71

Black-Scholes Merton Greeks

Spot Delta

CallΔcall=∂c∂S=e(b−r)TN(d1)>0PutΔput=∂p∂S=e(b−r)T[N(d1)−1]<0\begin{gathered} \text{Call} \\ \Delta_{\mathrm{call}}=\frac{\partial c}{\partial S}=e^{(b-r)T}N(d_{1})>0 \\ \mathbf{Put} \\ \Delta_{\mathrm{put}}=\frac{\partial p}{\partial S}=e^{(b-r)T}[N(d_{1})-1]<0 \end{gathered}

例如，考虑到期为六个月的期货期权。期货价格为105，行权价格为100，无风险利率为每年10％，波动率为每年36％。因此，S=105，X=100，T=0.5，r=0.1，b=0，σ=0.36S=105，X=100，T=0.5，r=0.1，b=0，\sigma=0.36。

d1=ln⁡(105/100)+(0+0.362/2)0.50.360.5=0.3189d_{1}={\frac{\ln(105/100)+(0+0.36^{2}/2)0.5}{0.36\sqrt{0.5}}}=0.3189

N(d1)=N(0.3189)=0.6251N(d_{1})=N(0.3189)=0.6251

Δcall=e(0−0,1)0.5N(d1)=0.5946\Delta_{\mathrm{call}}=e^{(0-0,1)0.5}N(d_{1})=0.5946

Δput=e(0−0.1)0.5[N(d1)−1]=−0.3566\Delta_{\mathrm{put}}=e^{(0-0.1)0.5}[N(d_{1})-1]=-0.3566

Forward Delta

Forward Delta的解释是，交易员需要购买多少单位（FOR）的远期合约来对冲一个空头期权：

ϕN(ϕd+)\phi\mathcal{N}(\phi d_+)

Strike From Delta（从Delta推到行权价）

在一些场外交易市场中，期权的报价是以Delta而不是行权价进行的。例如，在场外货币期权市场中，通常会询问一个Delta，并期望销售人员返回一个价格（以波动率或点数为单位），以及给定现货参考的行权价。在这些情况下，需要找到与给定Delta相对应的行权价。许多期权软件系统使用牛顿-拉弗森法或二分法对此进行数值求解。然而，实际上并不需要这样做。通过反转累积正态分布函数N−1(⋅)N^{-1}(\cdot)，可以从Delta中解析地推导出行权价，正如Wystrup（1999）所描述的那样。对于看涨期权

Xcall=Sexp⁡[−N−1(Δcalle(τ−b)T)σT+(b+σ2/2)T]X_{\mathrm{call}}=S\exp[-N^{-1}(\Delta_{\mathrm{call}}e^{(\tau-b)T})\sigma\sqrt{T}+(b+\sigma^{2}/2)T]

对于看跌期权：

Xput=Sexp⁡[N−1(−Δpute(r−b)T)σT+(b+σ2/2)T]X_{\mathrm{put}}=S\exp[N^{-1}(-\Delta_{\mathrm{put}}e^{(r-b)T})\sigma\sqrt{T}+(b+\sigma^{2}/2)T]

例如，为了使一个三个月的股票指数看涨期权的Delta达到0.25，假设无风险利率为7%，股息收益率为3%，波动率为50%，且股票指数交易价格为1800。给定参数为：S=1800，T=0.25，r=0.07，b=0.07−0.03=0.04，σ=0.5S=1800，T=0.25，r=0.07，b=0.07-0.03=0.04，\sigma=0.5。

通过计算可以得到：

N−1(Δcalfe(r−b)T)=N−1(0.25e(0.07−0.04)0.25)=−0.6686N^{-1}(\Delta_{\mathrm{calf}}e^{(r-b)T})=N^{-1}(0.25e^{(0.07-0.04)0.25})=-0.6686

然后，可以使用以下公式计算行权价：

Xcall=1800×exp⁡[0.6686×0.50.25+(0.04+0.52/2)0.25]=2217.0587X_{\mathrm{call}}=1800\times\exp[0.6686\times0.5\sqrt{0.25}+(0.04+0.5^{2}/2)0.25]=2217.0587

因此，为了使Delta达到0.25，需要将行权价设置为2217.0587。

Gamma

Gamma是对基础资产价格微小变动的Delta敏感性。Gamma对于看涨期权和看跌期权是相同的：

Γcall,put=∂2c∂S2=∂2p∂S2=n(d1)e(b−r)TSσT>0\Gamma_{call,put}=\frac{\partial^{2}c}{\partial S^{2}}=\frac{\partial^{2}p}{\partial S^{2}}=\frac{n(d_{1})e^{(b-r)T}}{S\sigma\sqrt{T}}>0

这是大多数教科书（如Hull（2005）和Wilmott（2000））中给出的标准伽玛度量。它衡量了在基础资产价格变动一个单位时Delta的变化。

例如，考虑到期为九个月的股票期权。股票价格为55，行权价为60，无风险利率为每年10％，波动率为每年30％。S=55，X=60，T=0.75S=55，X=60，T=0.75。

r=0.1,b=0.1,σ=0.3,which yieldsd1=ln⁡(55/60)+(0.1+0.32/2)0.750.30.75=0.0837n(d1)=n(0.0837)=12πe−0.08372/2=0.3975Γcall.put=0.3975e(0.1−0.1)0.7555×0.30.75=0.0278\begin{gathered} r=0.1,b=0.1,\sigma=0.3,\mathrm{which~yields} \\ d_{1}={\frac{\ln(55/60)+(0.1+0.3^{2}/2)0.75}{0.3\sqrt{0.75}}}=0.0837 \\ n(d_{1})=n(0.0837)=\frac{1}{\sqrt{2\pi}}e^{-0.0837^{2}/2}=0.3975 \\ \Gamma_{\mathrm{call.put}}=\frac{0.3975e^{(0.1-0.1)0.75}}{55\times0.3\sqrt{0.75}}=0.0278 \end{gathered}

Vega

Vega是期权对基础资产波动率微小变动的敏感性。对于看涨期权和看跌期权，维加是相同的。

Vegacall, put=∂2c∂σ2=∂2p∂σ2=Se(b−r)Tn(d1)T>0\mathrm{Vega}_{\mathrm{call,~put}}=\frac{\partial^2c}{\partial\sigma^2}=\frac{\partial^2p}{\partial\sigma^2}=Se^{(b-r)T}n(d_1)\sqrt{T}>0

图14绘制了维加随着基础资产价格和到期时间的变化的图形。

例如，考虑到期为九个月的股指期权，股指价格为55，行权价为60，无风险利率为每年10.50%，股息收益率为3.55%，波动率为每年30%。那么维加是多少？S=55，X=60，T=0.75，r=0.105S=55，X=60，T=0.75，r=0.105，b=0.105−0.0355=0.0695，σ=0.3b=0.105-0.0355=0.0695，\sigma=0.3，计算得到Vega的值为:

d1=ln⁡(55/60)+(0.0695+0.32/2)0.750.30.75=−0.0044d_{1}=\frac{\ln(55/60)+(0.0695+0.3^{2}/2)0.75}{0.3\sqrt{0.75}}=-0.0044

n(d1)=n(−0.0044)=0.3989n(d_1)=n(-0.0044)=0.3989

Vegacall,put=55e(0.0695⋅0.105)0.75×0.39890.75=18.5027\mathrm{Vega}_{\mathrm{call,put}}=55e^{(0.0695\cdot0.105)0.75}\times0.3989\sqrt{0.75}=18.5027

为了将其转换为对一百分之一波动率变动的Vega，我们需要将Vega除以100。因此，如果波动率从30%变化到31%，期权价值将大约增加0.1850。

Theta

Theta是期权对到期时间微小变动的敏感性。随着到期时间的减少，通常将Theta表示为对时间的偏导数的负值
Call

Θcall=−∂c∂T=−Se(b−r)Tn(d1)σ2T−(b−r)Se(b−r)TN(d1)−rXe−rTN(d2)≤≥0\begin{aligned}\Theta_{\mathrm{call}}&=-\frac{\partial c}{\partial T}=-\frac{Se^{(b-r)T}n(d_{1})\sigma}{2\sqrt{T}}-(b-r)Se^{(b-r)T}N(d_{1})\\&-rXe^{-rT}N(d_{2})\leq\geq0\end{aligned}

put

Θput=−∂p∂T=−Se(b−r)Tn(d1)σ2T+(b−r)Se(b−r)TN(−d1)+rXe−rTN(−d2) ≤≥ 0\begin{aligned}\Theta_{\mathrm{put}}&=-\frac{\partial p}{\partial T}=-\frac{Se^{(b-r)T}n(d_{1})\sigma}{2\sqrt{T}}+(b-r)Se^{(b-r)T}N(-d_{1})\\&+rXe^{-rT}N(-d_{2})\:\leq\geq\:0\end{aligned}

考虑一份欧式看跌期权，标的资产是目前定价为430的股票指数。行权价为405，到期时间为一个月，无风险利率为每年7%，股息收益率为每年5%，波动率为每年20%。S=430，X=405，T=0.0833，r=0.07，b=0.07−0.05=0.02，σ=0.2S=430，X=405，T=0.0833，r=0.07，b=0.07-0.05=0.02，\sigma=0.2，计算得到的结果是：

d1 = ln⁡(430/405)+(0.02+0.22/2)0.08330.20.0833 = 1.0952\begin{aligned}d_1\:=\:\frac{\ln(430/405)+(0.02+0.2^2/2)0.0833}{0.2\sqrt{0.0833}}\:=\:1.0952\end{aligned}

d2 = 1.0952−0.20.0833=1.0375d_{2}\:=\:1.0952-0.2\sqrt{0.0833}=1.0375

n(d1)=n(1.0952)=12πe−1.09522/2=0.2190n(d_1)=n(1.0952)=\frac1{\sqrt{2\pi}}e^{-1.0952^2/2}=0.2190

N(−d1)=N(−1.0952)=0.1367N(−d2)=N(−1.0375)=0.1498N(-d_1)=N(-1.0952)=0.1367\quad N(-d_2)=N(-1.0375)=0.1498

Oput=−430e(0.02−0.07)0.0833n(d1)0.220.0833+(0.02−0.07)430e(0.02−0.07)0.0833N(−d1)+0.07×405e−0.07×0.0833N(−d2)=−31.1924\begin{aligned} \text{Oput}& =\frac{-430e^{(0.02-0.07)0.0833}n(d_1)0.2}{2\sqrt{0.0833}} \\ &+(0.02-0.07)430e^{(0.02-0.07)0.0833}N(-d_{1}) \\ &+0.07\times405e^{-0.07\times0.0833}N(-d_2)=-31.1924 \end{aligned}

因此，每天的时间衰减Theta值为-31.1924/365=-0.0855。

Rho

Rho是期权对无风险利率微小变动的敏感性。

∂v∂rd=ϕKτe−rdτN(ϕd_)∂v∂rf=−ϕxτe−rfτN(ϕd+)\begin{gathered} \frac{\partial v}{\partial r_{d}} =\phi K\tau e^{-r_{d}\tau}\mathcal{N}(\phi d\_) \\ \frac{\partial v}{\partial r_f} =-\phi x\tau e^{-r}f^{\tau}\mathcal{N}(\phi d_{+}) \end{gathered}

Call

ρcalt=∂c∂r=TXe−rTN(d2)>0\rho_{\mathrm{calt}}=\frac{\partial c}{\partial r}=TXe^{-rT}N(d_{2})>0

ρcall=∂c∂r=−Tϵ<0\rho_{\mathsf{call}}=\frac{\partial c}{\partial r}=-T\epsilon<0

Put

ρput=∂p∂r=−TXe−rTN(−d2)<0\rho_{\mathrm{put}}=\frac{\partial p}{\partial r}=-TXe^{-rT}N(-d_{2})<0

例如，考虑一份欧式看涨期权，标的资产目前定价为72。行权价为75，到期时间为一年，无风险利率为每年9%，波动率为每年19%。因此，S=72，X=75，T=1，r=0.09，b=0.09，σ=0.19S=72，X=75，T=1，r=0.09，b=0.09，\sigma=0.19，

d2=ln⁡(72/75)+(0.09−0.192/2)10.191=0.1638N(d2)=N(0.1638)=0.5651ρcall=1×75ϵ−0.09×1N(d2)=38.7325\begin{aligned}d_2&=\frac{\ln(72/75)+(0.09-0.19^2/2)1}{0.19\sqrt{1}}=0.1638\\\\N(d_2)&=N(0.1638)=0.5651\\\\\rho_{\mathrm{call}}&=1\times75\epsilon^{-0.09\times1}N(d_2)=38.7325\end{aligned}

如果无风险利率从9%变化到10%，则看涨期权价格将增加约0.3873。

Vanna

∂2v∂σ∂x=−e−rfτn(d+)d−σ\frac{\partial^{2}v}{\partial\sigma\partial x}=-e^{-r_{f}\tau}n(d_{+})\frac{d_{-}}{\sigma}

Vanna有时也被称为dvegaldspotdvegaldspot。它反映了随着标的资产价格的变化，维加值的变化情况。交易员的Vanna假设标的资产价格相对变动为1%。Vanna这个术语的起源并不清楚。我怀疑它可以追溯到1990年代《风险杂志》上的一篇由蒂姆·欧文斯（Tim Owens）撰写的文章，他在文章中问道：“想要赔很多钱吗？”然后解释了如果不对冲二阶希腊字母（如Vanna和Volga）可能会造成损失的情况。

Volga

∂2v∂σ2=xe−rfττn(d+)d+d−σ\frac{\partial^{2}v}{\partial\sigma^{2}}=xe^{-r}f^{\tau}\sqrt{\tau}n(d_{+})\frac{d_{+}d_{-}}{\sigma}

Volga有时也被称为υomma\upsilon omma或υolgamma\upsilon olgamma或dvegaldvoldvegaldvol。Volga反映了随着波动率变化，维加值的变化情况。交易员的Volga假设波动率的绝对变动为1%。

Numerical Greeks（数值方法计算敏感性）

到目前为止，我们只看过解析希腊字母（Analytical Greeks）。一个经常使用的替代方法是使用数值希腊字母，也称为有限差分逼近法（Finite Difference Approximations）。数值希腊字母的主要优势在于，它们的计算与考虑的模型无关。只要我们有一个准确的模型来计算导数的值，有限差分逼近法就能给出我们所需要的希腊字母值。

First-Order Greeks（一阶希腊字母）

一阶偏导数∂f(x)∂x\frac{\partial f(x)}{\partial x}可以通过双边有限差分法来近似计算：

c(S+ΔS,X,T,r,b,σ)−c(S−ΔS,X,T,r,b,σ)2ΔS\frac{c(S+\Delta S,X,T,r,b,\sigma)-c(S-\Delta S,X,T,r,b,\sigma)}{2\Delta S}

对于关于时间的导数，我们知道时间的移动方向，并且使用后向导数（单边有限差分）更准确（对于“真实”世界中发生的情况）。即：

Θ≈c(S,X,T,r,b,σ)−c(S,X,T−ΔT,r,b,σ)ΔT\Theta\approx\frac{c(S,X,T,r,b,\sigma)-c(S,X,T-\Delta T,r,b,\sigma)}{\Delta T}

数值希腊字母相比解析希腊字母有几个优点。例如，如果我们有一个固定的Delta波动率曲线（sticky delta volatility smile），那么在计算数值Delta时我们可以相应地改变波动率。（当波动率曲线根据标的资产价格变化而变动时，我们称之为固定Delta波动率曲线；换句话说，给定行权价的波动率会随着标的资产价格的变动而移动。）

Δcall≈c(S+ΔS,X,T,r,b,σ1)−c(S−ΔS,X,T,r,b,σ2)2ΔS\Delta_{\mathrm{call}}\approx{\frac{c(S+\Delta S,X,T,r,b,\sigma_{1})-c(S-\Delta S,X,T,r,b,\sigma_{2})}{2\Delta S}}

此外，数值希腊字母是与模型无关的，而上述的解析希腊字母是特定于BSM模型的。

Second-Order Greeks（二阶希腊字母）

对于速度和其他三阶导数∂3f(x)∂x3\frac{\partial^3f(x)}{\partial x^3}，我们可以使用以下逼近方法：

Speed≈1ΔS3[c(S+2ΔS,…)−3c(S+ΔS,…)+3c(S,…)−c(S−ΔS,…)]\mathrm{Speed}\approx\frac{1}{\Delta S^{3}}[c(S+2\Delta S,\ldots)-3c(S+\Delta S,\ldots)+3c(S,\ldots)-c(S-\Delta S,\ldots)]

Mixed Greeks（混合希腊字母）

对于混合导数∂f(x,y)∂x∂y\frac{\partial f(x,y)}{\partial x\partial y}，例如

DdeltaDvol≈14ΔSΔσ×[c(S+ΔS,…,σ+Δσ)−c(S+ΔS,…,σ−Δσ)−c(S−ΔS,…,σ+Δσ)+c(S−ΔS,…,σ−Δσ)]\begin{aligned}\text{DdeltaDvol}&\approx\frac{1}{4\Delta S\Delta\sigma}\\&\times[c(S+\Delta S,\ldots,\sigma+\Delta\sigma)-c(S+\Delta S,\ldots,\sigma-\Delta\sigma)\\&-c(S-\Delta S,\ldots,\sigma+\Delta\sigma)+c(S-\Delta S,\ldots,\sigma-\Delta\sigma)]\end{aligned}

DdeltaDvol和charm，可以通过数值计算来获得。对于DdeltaDvol，通常会将其除以100以得到“正确”的表示法，即对于波动率的一点变动。

Third-Order Mixed Greeks（三阶混合希腊字母 ）

对于像DgammaDvol这样的希腊字母，我们需要计算三阶混合希腊字母∂3f(x,y)∂x2∂y\frac{\partial^3f(x,y)}{\partial x^2\partial y}：

DgammaDvol≈12ΔσΔS2×[c(S+ΔS,…,σ+Δσ)−2c(S,…,σ+Δσ)+c(S−ΔS,…,σ+Δσ)−c(S+ΔS,…,σ−Δσ)+2c(S,…,σ−Δσ)−c(S−ΔS,…,σ−Δσ)]\begin{aligned} \text{DgammaDvol}& \approx\frac{1}{2\Delta\sigma\Delta S^{2}} \\ &\times[c(S+\Delta S,\ldots,\sigma+\Delta\sigma)-2c(S,\ldots,\sigma+\Delta\sigma) \\ &+c(S-\Delta S,\ldots,\sigma+\Delta\sigma)-c(S+\Delta S,\ldots,\sigma-\Delta\sigma) \\ &+2c(S,\ldots,\sigma-\Delta\sigma)-c(S-\Delta S,\ldots,\sigma-\Delta\sigma)] \end{aligned}

对于DgammaDvol，通常也会将其除以100以得到“正确”的表示法。

采用数值计算方法计算Delta

raw delta = (v₁ – v₂) / (2 × bump)

这里：

  • raw delta

    • 由有限差分方法计算：
      raw delta = (v₁ – v₂) / (2 × bump)
    • 这里的 v₁ 与 v₂ 分别是 bump 上下调后的期权价格，而 bump 是 spot 的单位变化量。

  • premium adjusted delta（调整后的 delta）

    • 考虑了期权 premium 对敏感性的影响。
    • 对于外汇期权而言，通常需扣除期权价格相对于 spot 的比例。

  • ccy2 delta

    • 一般指以外币计价的 delta。
    • 定义为：
      ccy2 delta = raw delta

  • ccy1 delta

    • 指以本币计价的 delta，表达为：
      ccy1 delta = raw delta – v₀/S
    • 其中 v₀ 是期权价格，S 是当前的 spot 汇率。

美式期权如何计算forwrd delta？

有些期权的计算模型，比如：美式期权BAW或PDE模型，计算参数中，均未有forward，所以，无法直接通过改变forward来计算forward delta。
下面给出一种常用的方法，通过 bump and reprice 来获得外汇美式期权的 forward delta。关键在于认识到：

Forward = S × exp[(r_d – r_f) × (T – t)]

若你的定价程序中只提供了 S、r_d 和 r_f，那 forward 并没有作为单独的输入参数传入，但可以根据上述公式计算得出 forward。

  1. 基本思路

假设你希望计算 forward delta，即期权价格对于 forward 的敏感性，记作
  Δ_F = ∂V/∂F

由于 forward 与 spot 的关系为
  F = S × exp[(r_d – r_f) × (T – t)]
因而利用链式法则有

Δ_F = (∂V/∂S) × (∂S/∂F)
      = Δ_S / exp[(r_d – r_f) × (T – t)]

其中 Δ_S = ∂V/∂S 是传统的 spot delta。

  1. Bump and Reprice 计算方法

使用 bump and reprice 方法，可以按下面步骤进行：

  1. 计算基准价格
      用当前的 S、r_d、r_f 定价，得到期权价格 V(S)。

  2. 确定 bump 大小
      假设希望 bump 的是 forward，仅 bump forward ΔF。如前所述，由于 F 与 S 的关系为
        ΔF = exp[(r_d – r_f) × (T – t)] × ΔS
      因此，为了 bump forward ΔF，你需要将 S 增加
        ΔS = ΔF / exp[(r_d – r_f) × (T – t)]

  3. 计算 bumped 价格
      令新的 spot 为 S_bumped = S + ΔS，然后用新的 spot 重新跑 FDM 模型得到 bumped 的价格 V(S_bumped)。

  4. 计算 spot delta
      Δ_S ≈ [V(S_bumped) – V(S)] / ΔS

  5. 换算 forward delta
      按照链式法则，forward delta 为
        Δ_F ≈ Δ_S / exp[(r_d – r_f) × (T – t)]
      或等价的，直接用 bump forward 后的价格变化：
        Δ_F ≈ [V(S_bumped) – V(S)] / ΔF

两种方式在 ΔS 与 ΔF 的换算关系下是一致的，关键是 bump 的时刻要对应 forward 的改变，而不是简单地对 S 做绝对 bump。

  1. 小结
  • 由于外汇 forward 与 spot 的关系 F = S × exp[(r_d – r_f)(T – t)]，所以当你想通过 bump and reprice 算出 forward delta 时，可以根据 forward 的 bump 来计算相应 spot 的 bump。
  • 具体方法为：设定 forward bump ΔF，计算出相应的 ΔS，再重新定价获得 V(S_bumped)，由此得出 spot delta，再除以 exp[(r_d – r_f)(T – t)] 得到 forward delta。
  • 也可以直接将 bump 值在价格变化上写为：
      Δ_F ≈ [V(S + ΔS) – V(S)] / ΔF

这样，即使程序参数中没有显式传入 forward，也能通过 spot 的 bump 过程推导出 forward delta。

定价、估值与风险管理
Copyright © 2025 上海子午线