外汇亚式期权 – 定价原理

上海子午线大约 13 分钟

外汇亚式期权 – 定价原理

访问猛犸期权定价系统，支持外汇期权和结构化产品定价估值！

外汇亚式期权的简介，可以参考文章《外汇亚式期权》。

亚式期权是一种期权合约，其收益由标的在一段时间内的平均值决定。亚式期权在场外能源市场和其他缺乏流动性的大宗商品市场中很受欢迎。事实上，平均意味着价格波动性降低，期权价格更便宜，市场操纵的可能性较小。

亚式期权可以按多个维度进行分类，即：

平均价类型：平均行行权价（average strike or floating strike）、平均观察价格（average rate or fixed strike）
平均价计算：算术平均(Arithmetic)、几何平均(Geometric)
平均价日期：离散(Discrete)、连续(Continue)，对于离散方式，观察日期通常由开始时间（Average Start）、以及观察周期（Frequency）来确定；连续观察日期，是指从期权开始日期到到期日，每一天都是观察日（Fixing Date）
行权方式：美式行权(American)、欧式行权(European)

考虑到存续期的亚式期权，也会有下面方式的的划分，这样划分的目的是这两种期权在通过封闭解（Closed Form）进行求解时，使用到了不同的计算模型

未进入到平均价期间的亚式期权
已经进入到平均价期间的亚式期权

这里把定价和估值相关参数列示如下：

参数	Parameters	示例	注释
看涨/看跌	Call/Put	Call	Call/Put
行权价类型	Strike Type	Fixed	Fixed/Floating
平均价计算方式	Average Type	Arithmetic	Arithmetic/Geometric
行权方式	Exercise Type	European	European/American
计算日期（交易日期）	Reference Date	2022/10/8
期权费日期	Premium Date	2022/10/10
到期日期	Expiry Date	2023/10/8
结算日期	Settlement Date	2023/10/10
即期价格	Spot	6.8
行权价格	Strike	6.9
初次平均价日期	First Average Date	2022/05/24	初次平均价可能不等于计算日期（或交易日期）
平均价周期	Fixing Frequency	Monthly	Daily, Weekly, Monthly
累计平均价	Average Rate	7.0	对于存续期交易、并已经进入到平均价期间的交易，累计平均价是累计的观察日期的平均价格
平均价次数	Number of Fixings	12	根据初次平均价日期、到期日、平均价周期计算
完成平均价次数	Number of Fixing Done	2	根据平均价日期、计算日期、到期日期、平均价周期计算

平均行权价和平均观察价格

两种方式下，到期行权的回报计算方式如下：

到期回报（Payoff）	Call	Put
平均行权价	max (S-A, 0)	max (A-S, 0)
平均观察价格	max (A-X, 0)	max (X-S, 0)

这里：

S – Underlying Price
X – Exercise Price (Strike)
A – Average Price (Strike or Rate)

几何平均和算数平均

算数平均价计算方式：

Average_{Arithmetic}=\frac{\sum_{i=1}^nS_i}n

几何平均价计算方式：

Average_{\text{Geometr}ic}=\sqrt[n]{\prod_{i=1}^nS_i}

在实际应用中，由于是连乘方式，上述公式很容易会导致计算过程中数据类型越界，所以通常采用下面方式来替换[i]：

Average_{Geometric}=e^{\frac{\sum_{i=1}^n\log S_i}n}

平均价日期（定价日期）（离散）

平均价日期，是根据初次平均价日期、到期日、平均价周期计算得到，计算时需要考虑残端方式（前置、后置）、以及节假日。

得到平均价（定价）日期后，还需要根据计算日期来计算平均价次数（通常用n表示）、以及完成平均价次数（通常用j表示），这两个参数会在利用封闭解方式定价时用到。

定价和估值

亚式期权通常有几种定价方式：

封闭解方式定价（Analytical Model）
二叉树方式定价（Binomial Model）
三叉树方式定价（Trinomial Model）
PDE模型定价
蒙特卡洛方式定价（Monte-Carlo Model）

这里重点介绍解析解、以及蒙特卡洛方式定价。

封闭解方式

不同于欧式期权的BSM模型，不同平均价计算方式、以及平均价类型的期权需要采用不同的近似计算模型来求解。这里整理部分模型：

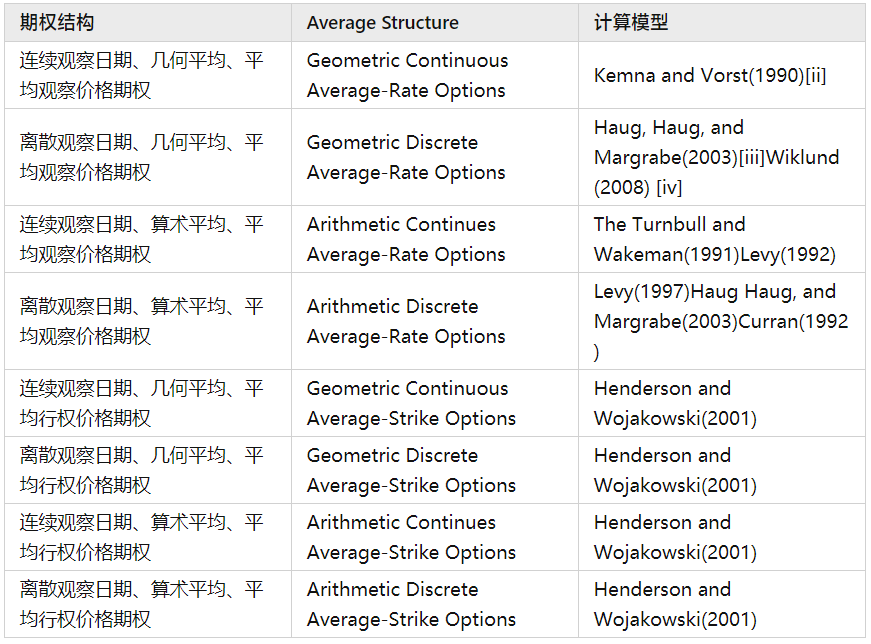
离散观察日期、几何平均、平均观察价格期权（Geometric Discrete Average-Rate Options）

因为几何平均值同市场价格变化都有共同特性，符合对数正态分布，所以，可以推导出来一个封闭的公式来对几何平均价格期权进行定价。

这里直接列出Wiklund (2012) 在_Asian Option Pricing and Volatility_ 一文中，对Geometric Asian Option的定价公式：

c=S_{0}A_{j}N\big(d_{n-j}+\sigma\sqrt{T_{2,n-j}}\big)-Ke^{-\gamma T}N(d_{n-j})

p=Ke^{-rT}N(-d_{n-j})-S_{0}A_{j}N\big(-d_{n-j}-\sigma\sqrt{T_{2,n-j}}\big)

这里：

d_{n-j}=\frac{ln\left(\frac{S_{0}}{K}\right)+\left(r-q-\frac{\sigma^{2}}{2}\right)T_{1,n-j}+ln(B_{j})}{\sigma\sqrt{T_{2,n-j}}}

A_{j}=e^{-r(T-T_{1,n-j})-\sigma^{2}(T_{1,n-j}-T_{2,n-j})/2}B_{j}

T_{1,n-j}=\frac{n-j}{n}(T-\frac{(n-j-1)h}{2})

T_{2,n-j}=\left(\frac{n-j}{n}\right)^{2}T-\frac{(n-j)(n-j-1)(4n-4j+1)}{6n^{2}}h

B_{j}=\left(\prod_{i}^{j}\frac{S[T-(n-j)h]}{S}\right)^{1/n},B_{0}=1

其中_S(T-(n-j)h)_是在T-(n-j)*h时刻，也就是过去日期的观察价格，符几何布朗运动（Geometric Brown Motion）。

在Peter G. Zhang(1998)[v]中对S(T)的定义为：

S[T-(n-j)h]=S\exp\left(\left(r-q-\frac{1}{2}\sigma^{2}\right)[T-(n-j)h]+\sigma z[T-(n-j)h]\right)

这里：z(T)是标准的高斯分布（Standard Gauss-Random）。

代码实现如下（Python）

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Apr 27 05:24:55 2022

@author: larrychen
"""
from math import log, sqrt, exp
from scipy.stats import norm

def GeometricAverageRate(CallPutFlag, S, SA, X, T, Tf, r, q, v, j, n ):
  
  if (CallPutFlag == 'c'):
  w = 1
  else:
   w = -1
  
  h = (T + Tf) / (n - 1)  #fix frequency
  Bj = BSA(S, SA, T, Tf, n, j, h, v, r, q)
  
  T1 = (n - j) / n * (T - h * (n - j - 1) / 2)
  T2 = T * ((n - j) / n) ** 2 - (n - j) * (n - j - 1) * (4 * n - 4 * j + 1) * h / (6 * n * n)
  
  Aj = exp(-r * (T - T1) - v * v * (T1 - T2) / 2) * Bj  
  d = (log(S / X) + (r - q - v * v / 2) * T1 + log(Bj)) / (v * sqrt(T2))
  
  return w * S * Aj * exp(-q * T1) * norm.cdf(w * d + w * v * sqrt(T2)) - w * X * exp(-r * T) *norm.cdf(w * d)

  
def BSA(S, SA, T, Tf, n, j, h, v, r, q):
  # for Geometric Average option
  # SA - if T is into average period, SA is fixed fixing average price

  Bj = 1
  
  if (j == 0):
  Bj = 1
  else:
  Bj = (SA / S) ^ (j / n)
  
  return Bj

import numpy as np
import matplotlib.pyplot as plt
# testing 
CallPutFlag = 'c'  #Call='c', Put='p'
S=6.8  #SpotPx
X=6.9  #StrikePx
SA=7.0  #AverageRate, cumulative average rate
T=1.3808  #TimeToExpiry
Tf=-0.3808  #Time from First Fixing to Calculation day
r=0.07  #risk-free rate or demostic rate
q=0.05  #dividend or foreign rate
v=0.2  #Volatility
n=13  #Number of Fixings
j=0  #Number of Fixings Done

premium = GeometricAverageRate(CallPutFlag, S, SA, X, T, Tf, r, q, v, j, n )
print ('Geometric Average-Rate Asian Optin, Premium=')
print (premium)

vGeometricAverageRate = np.vectorize(GeometricAverageRate)
x=np.arange(100)/100 + 6.3
px=vGeometricAverageRate(CallPutFlag, x, SA, X, T, Tf, r, q, v, j, n)
plt.plot(x,px)

算术平均、平均行权价格期权（Arithmetic Average-Strike Options）

算术平均并不符合对数正态分布的特征，所以理论上不可能获得一个封闭解来对算术平均亚式期权进行定价。但是还是可以利用几何平均来近似求解算术平均亚式期权。Haug Haug, and Margrabe(2003)、Levy(1997)、Wiklund(2012)均提出了相应的求解公式。这里不在重复列出。

蒙特卡洛方式

蒙特卡洛应用在期权定价的模拟最初是由Boyle在1977年提出来，其实质是通过模拟标的资产价格路径预测期权的平均回报并得到期权价格估计，蒙特卡洛特别适用于多维度的复杂期权定价，并且相对比较准确能反映出产品的特性，所以如果有足够的模拟次数，能相对准确计算出产品价格，并且随着计算机算力的增强，特别是近些年GPU的应用，蒙特卡洛的应用越来越广泛。

由于亚式期权的结构复杂性，存在不同平均价方式（几何平均、算术平均）、平均价类型（观察价格、行权价格）、是不是已经进入了观察周期等多个不同的场景、所以并不存在一个封闭解公式适应所有的场景，通常需要4-5个不同的公式来结合使用，并且特别是对于进入观察周期的期权，由于存在已经确定的平均价（累计平均价），封闭解公式并不能对累积平均价做好的处理，这里封闭解公式对实际场景的定价准确性存在一些疑问。所以，采用蒙特卡洛方式对亚式期权定价是一个很好的补充。

蒙特卡洛的计算有几个步骤：

步骤一：确定Payoff

步骤二：生成模拟市场数据

步骤三：根据市场数据来生成payoff结果、并计算NPV

确定payoff

确定回报的计算方式，这里分为几种情况（下面只讨论离散方式的亚式期权）：

一、平均观察价格（Average Rate）期权，看涨或看跌期权

Payoff_{average-rate,call}=(A_{rate}-K)^{+}

Payoff_{average-rate,put}=(K-A_{rate})^{+}

这里 $A_{rate}$ 为平均观察价格，分为算术平均或几何平均：

A_{rate,arithmetic}=\frac1{m+1}\Bigg(A_0+\sum_{j=0}^mS(t_j)\Bigg)

或

A_{rate,geometric}=\exp\left(\frac{log(A_0)+\sum_{j=0}^mlog\left(S(t_j)\right)}{m+1}\right)

这里 $A_{0}$ 为已累计平均值，也就是在进入观察期到计算日之间已经确定的累积平均值，m为未来定价日数量，

$t_{j}$ 为未来定价日， $S\left(t_{j}\right)$ 为未来定价日的模拟价格。

二、平均行权价格（Average Strike）期权

Payoff_{average-strike,call}=(S(T)-A_{strike})^{+}

Payoff_{average-strike,put}=\left(A_{strike}-S(T)\right)^{+}

这里 $S\left(t\right)$ 为最后一天（到期日）的模拟价格， $A_{rate}$ 为平均行权价格，分为算术平均或几何平均：

A_{strike,arithmetic}=\frac1{m+1}{\left(A_0+\sum_{j=0}^mS(t_j)\right)}

或

A_{strike,geometric}=\exp\left(\frac{log(A_0)+\sum_{j=0}^mlog\left(S(t_j)\right)}{m+1}\right)

这里 $A_{0}$ 为已累计平均值，也就是在进入观察期到计算日之间已经确定的累积平均值，m为未来定价日数量，

$t_{j}$ 为未来定价日， $S\left(t_{j}\right)$ 为未来定价日的模拟价格。

生成模拟市场价格

根据Winner Process原理来生成模拟市场价格，市场价格的分布符合布朗运动：

S_i(t_h)=S(0)e^{\left[\left(r-q-\frac12\sigma^2\right)t_h+\sigma\sqrt{t}z_i\right]}

这里1 $\leq i\leq N$ ,N为模拟次数（PATH），1 $\leq h\leq H$ ,H为步长（time step），通过上述公式生成N x H组模拟价格，如下图：

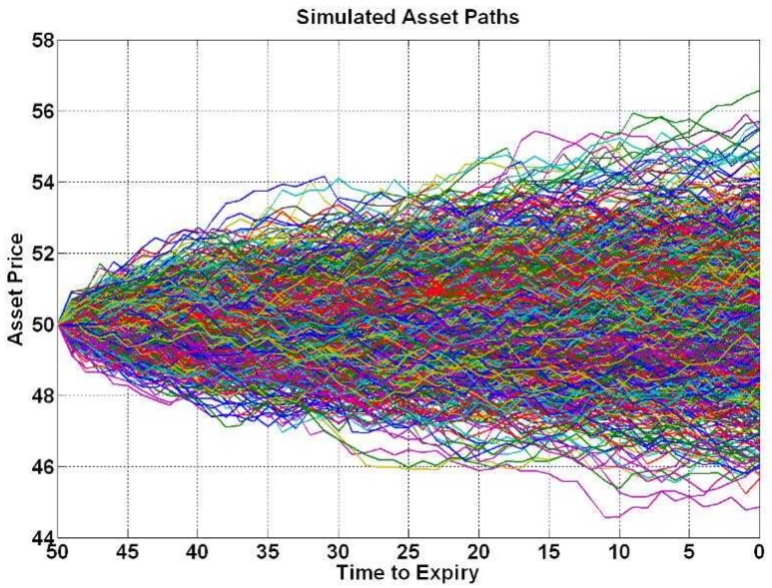
根据市场数据来生成payoff结果、以及NPV

根据Payoff结果生成NPV

NPV=\frac1N{\left(\sum_i^NPayoff_i\right)}e^{-rT}

这里NPV就是最终的期权价格。

封闭解和蒙特卡洛的结果对比

这里采用Wiklund（2012）对几何平均、平均观察价格期权（Geometric Average-Rate Asian Option）的定价方式，对比蒙特卡洛模拟结果。

采用的计算参数如下：

参数	Wirklund(2012)	蒙特卡洛模拟	场景
BuySell	Buy	Buy
CallPut	Call	Call	Call / Put
SpotPx	6.8	6.8	6.3 – 6.8
StrikePx	6.9	6.9
StrikeType	Fixed	Fixed
ReferenceDate	2022/5/24	2022/5/24	2022/5/24 -2022/12/24
FirstAverageDate	2022/10/10	2022/10/10
ExpiryDate	2023/10/10	2023/10/10
SettlementDate	2023/10/12	2023/10/12
AveRate	7	7
PricingMethod	BLACKSCHOLES	MONTECARLO
KeepEndOfMonth	FALSE	FALSE
FixingFrequency	Monthly	Monthly
FixingDateAdjuster	ModifiedFollowing	ModifiedFollowing
FixingLongStub	FALSE	FALSE
FixingEndStub	TRUE	TRUE
Calendar	McpCalendar@5	McpCalendar@5
DayCounter	Act365Fixed	Act365Fixed
FaceAmount	1	1
premiumDate	2022/12/24	2022/12/24
NumSimulation		100000
DomesticRate	0.07	0.07
ForeignRate	0.05	0.05
volatility	0.2	0.2

上述期权结构的定价日为：

场景一：即期价格变化同期权费用的关系：

设定期权类型为：看涨期权（Call）、计算日期为2022/5/24，其他要素见上面表格，改变即期价格，观察对期权价值的影响。

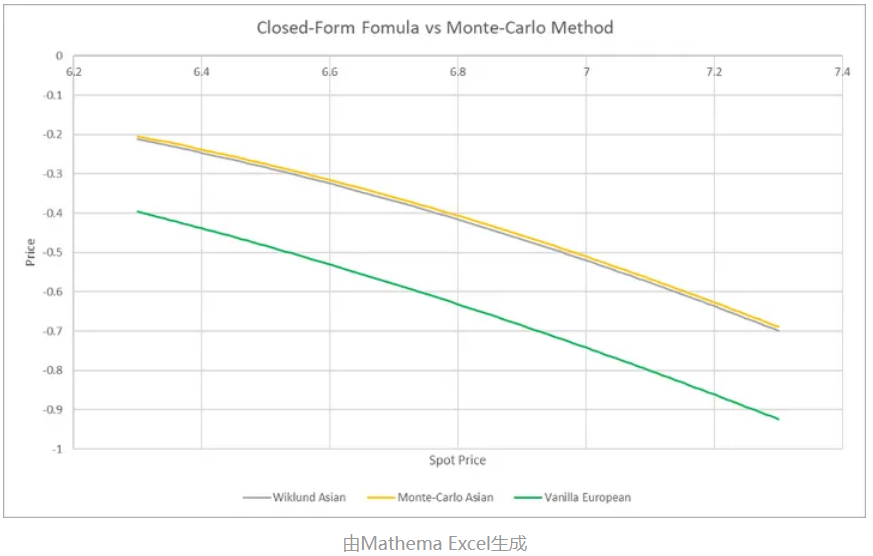
封闭解同蒙特卡洛模拟结果基本一致，对比同条件下欧式期权，亚式期权的费用要比欧式期权低（-20%～-50%）。

场景二：看涨期权，计算日期变化同期权价格的关系

设定期权类型为：看涨期权（Call）、即期价格为6.8，其他要素见上面表格，改变计算日期，观察对期权价值的影响。

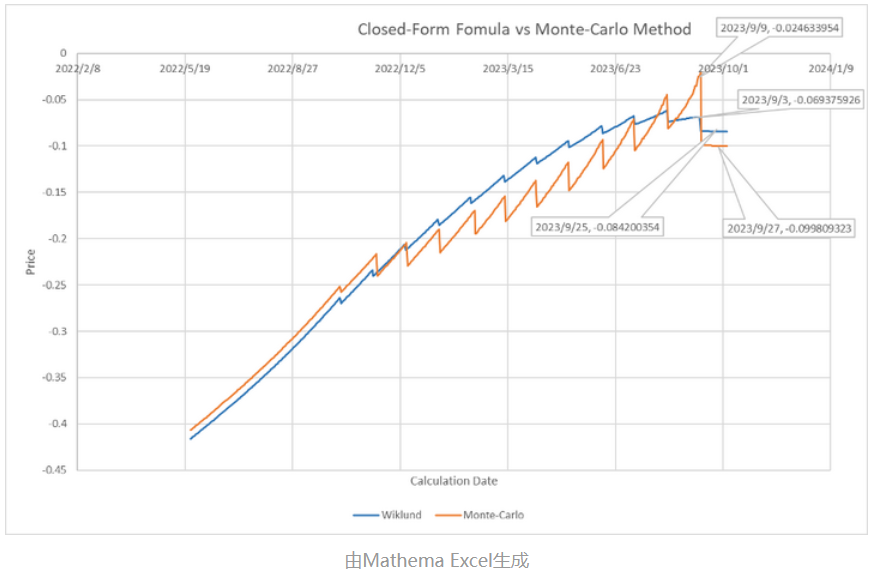
根据我们对下面两个场景的观察：

2023年9月9日	2023年9月15日
分析：当前累计的平均价格为7.0、即期价格6.8，可以预测9月11日的观察价格应该～6.8，所以平均价价格应该在6.9左右。9月11日是最后一次确定平均价日期，确定后，到期累计市场价格、以及行权价被确定，期权价值也基本上被确定，所以这是的期权价格应该为9月11日到期，即期价格6.8、行权价应该在6.85左右的期权价格，通过欧式期权来估算，为0.029，所以估算当时的期权价格应该在0.02～0.03之间	分析：已经确定了到期累计观察价格为6.9[=(6.8+7.0)/2]，行权价为0.1，所以从9月11到10月10日的期权费用为0.1的折现价值

2023年9月9日

2023年9月15日

分析：当前累计的平均价格为7.0、即期价格6.8，可以预测9月11日的观察价格应该～6.8，所以平均价价格应该在6.9左右。9月11日是最后一次确定平均价日期，确定后，到期累计市场价格、以及行权价被确定，期权价值也基本上被确定，所以这是的期权价格应该为9月11日到期，即期价格6.8、行权价应该在6.85左右的期权价格，通过欧式期权来估算，为0.029，所以估算当时的期权价格应该在0.02～0.03之间

分析：已经确定了到期累计观察价格为6.9[=(6.8+7.0)/2]，行权价为0.1，所以从9月11到10月10日的期权费用为0.1的折现价值

封闭解方式	蒙特卡洛方式	封闭解方式	蒙特卡洛方式
期权价格为0.069，同估算不一致	期权价格为0.025，同估算基本一致	期权价格为0.084，同估算不一致	期权价格为0.0998，很好反映估算情况

根据上述估算，我们可以大胆给出相应的结论：在这个场景下，封闭解方式，并不能实际真实反映市场状况，特别是在期权接近最后一次观察日、以及到期日。

场景三：看跌期权，计算日期变化同期权价格的关系

设定期权类型为：看跌期权（Put）、即期价格为6.8，其他要素见上面表格，改变计算日期，观察对期权价值的影响。

这个场景中，我们引入简单欧式期权价格作为参考。

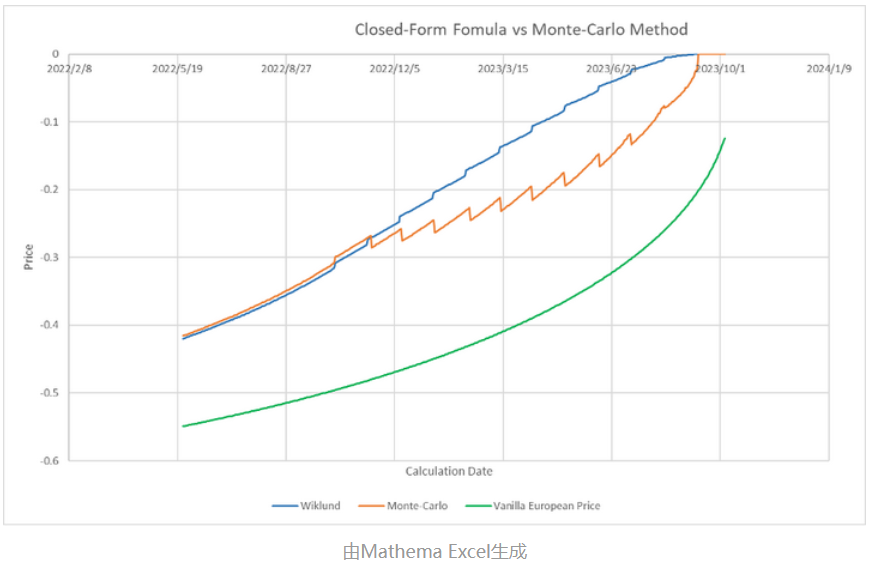
根据对比结果，可以看出在进入观察期以后，两种模型的计算结果差别比较大（～10%），我们无法判断结果准确性，这里对比欧式期权的结果供读者自行判断。

蒙特卡洛的算力比较（GPU vs CPU）

随着计算机性能的提升，以及GPU的应用，蒙特卡洛的算力通过多线程、以及GPU技术，可以得到大幅度提升，根据下面对比测试，相比单线程方式，算力可以提升500-700倍。

输入参数，可以参考上面表格。根据测试结果，可以看出蒙特卡洛在保证机器配置的前提下，完全可以替代封闭解方式。

模拟次数	封闭解	蒙卡（单线程）	蒙卡（多线程（10核））	蒙卡（GPU）
10万	0.168秒	1.2秒	0.112秒	0.012秒
100万	0.168秒	9.2秒	0.902秒	0.013秒
1000万	0.168秒	90秒	8.30秒	0.223秒

CPU：Intel(R) Core(TM) i9-10900K CPU @ 3.70GHz

GPU：NVIDIA GeForce RTX 3080 Ti

我们提供亚式期权方案：

子午线亚式期权方案